高中數學公式表
乘法公式
\[ \begin{array}{rcl} (a+b)^2&=&a^2+2ab+b^2, \\ (a-b)^2&=&a^2-2ab+b^2, \\ a^2+b^2&=&(a+b)^2-2ab=(a-b)^2+2ab, \\ a^2-b^2&=&(a+b)(a-b), \\ (a+b)^3&=&a^3+3a^2b+3ab^2+b^3, \\ (a-b)^3&=&a^3-3a^2b+3ab^2-b^3, \\ a^3+b^3&=&(a+b)(a^2-ab+b^2), \\ a^3-b^3&=&(a-b)(a^2+ab+b^2), \\ \end{array} \]分點公式
| 數線上 \(A=x_1, B=x_2\) | 平面直角坐標上 \(A=(x_1, y_1), B=(x_2, y_2)\) | 空間直角坐標上 \(A=(x_1, y_1, z_1), B=(x_2, y_2, z_2)\) | |
| \(\overline{AB}\) 線段中點 \(M\) 的坐標 | \(M=\frac{x_1+x_2}{2}\) | \(M=\left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}\right)\) | \(M=\left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}, \frac{z_1+z_2}{2}\right)\) |
| \(\overline{AB}\) 線段內分點 \(C\) 的坐標，其中 \(\overline{AC}:\overline{CB}=m:n\) | \(C=\frac{x_1 n+x_2 m}{m+n}\) | \(C=\left(\frac{x_1 n+x_2 m}{m+n}, \frac{y_1 n+y_2 m}{m+n}\right)\) | \(C=\left(\frac{x_1 n+x_2 m}{m+n}, \frac{y_1 n+y_2 m}{m+n}, \frac{z_1 n+z_2 m}{m+n}\right)\) |
絕對值的定義
\[ |x|=\left\{ \begin{array}{ll} x, & x\geq 0; \\ -x, & x<0. \end{array} \right. \]絕對值的幾何意義
\(|a-b|\) 表示數線上兩點 \(a\) 跟 \(b\) 之間的距離。平方再開平方根
\[ \sqrt{a^2}=|a|. \]雙重根號
\[ \begin{array}{rcl} \sqrt{(a+b)+2\sqrt{ab}}=\sqrt{a}+\sqrt{b}, \\ \sqrt{(a+b)-2\sqrt{ab}}=\sqrt{a}-\sqrt{b}. \end{array} \]大一新鮮人的夢
\[ \begin{array}{rcl} (a+b)^2 &\neq & a^2+b^2,\\ (a\times b)^2 &=& a^2\times b^2, \\ \sqrt{a^2+b^2} &\neq & a+b, \\ \sqrt{a^2\times b^2} &= & |a|\times |b|. \end{array} \]無限循環小數化成分數
算幾不等式
\[ \frac{\square+\triangle}{2}\geq \sqrt{\square\triangle} \]指數律
- \(a^m a^n=a^{m+n}\)
- \(\frac{a^m}{a^n}=a^{m-n}\)
- \((ab)^m=a^m b^m\)
- \(\left(\frac{a}{b}\right)^m=\frac{a^m}{b^m}\)
- \((a^m)^n=a^{mn}\)
- \(a^{-1}=\frac{1}{a}\)
- \(a^{\frac{m}{n}}=\sqrt[n]{a^m}\)
另一種背法
| 相乘 | 相除 | |
| 同底 | \(a^m a^n=a^{m+n}\) | \(\frac{a^m}{a^n}=a^{m-n}\) |
| 同指 | \((ab)^n=a^n b^n\) | \(\left(\frac{a}{b}\right)^n=\frac{a^n}{b^n}\) |
對數律
- \(\log_{a}xy=\log_a{x}+\log_a{y}\)
- \(\log_{a}\frac{x}{y}=\log_a{x}-\log_a{y}\)
- \(\log_{a}x^m=m\log_a{x}\)
- \(\log_{a^n}x=\frac{1}{n}\log_a{x}\)
- \(\log_{a}x=\frac{\log_{b}x}{\log_{b}a}\)
- \(a^{\log_{a}x}=x\)
直線的斜率
平面上通過 \(A=(x_1, y_1), B=(x_2, y_2)\) 兩點的直線的斜率為 \[ \frac{y_2-y_1}{x_2-x_1} \]由斜率求直線的方程式
平面上通過點 \(P=(x_1, y_1)\) 且斜率為 \(m\) 的直線方程式為 \[ y-y_1=m(x-x_1) \]由直線的方程式求斜率
方程式為 \(y=mx+b\) 的直線斜率為 \(m\)。垂直直線的斜率關係
平面上兩直線 \(L_1\) 及 \(L_2\)，假設直線 \(L_1\) 的斜率為 \(m_{L_1}\)，直線 \(L_2\) 的斜率為 \(m_{L_2}\)。若兩直線平行，則 \(m_{L_1}=m_{L_2}\)。
若兩直線垂直，則 \(m_{L_1}m_{L_2}=-1\)。
三角形的重心與內心坐標
\(\triangle ABC\) 中，\(A(x_1, y_1), B(x_2, y_2), C(x_3, y_3)\)，\(\overline{AB}=c, \overline{BC}=a, \overline{CA}=b\)，則內心 \(I\) 坐標為 \[ I=\left(\frac{ax_1+bx_2+cx_3}{a+b+c}, \frac{ay_1+by_2+cy_3}{a+b+c}\right) \]
重心 \(G\) 坐標為 \[ G=\left(\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3}\right) \]
點與直線的距離公式
平面上一點 \(P=(x_1, y_1)\)，一直線 \(L:ax+by+c=0\)，則點 \(P\) 到直線 \(L\) 的距離為 \[ \frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}} \]兩平行線的距離公式
平面上兩直線 \(L_1:ax+by+c_1=0\) 及 \(L_2:ax+by+c_2=0\)，則兩直線的距離為 \[ \frac{|c_1-c_2|}{\sqrt{a^2+b^2}} \] 注意到兩直線方程的 \(x, y\) 係數必須變形為相同。圓方程式
回憶到兩點 \(P(x_1, y_1), Q(x_2, y_2)\) 的距離公式為 \[ \sqrt{(x_2-x_1)^2+(y_2-y_1)^2} \] 圓心在 \((x_1, y_1)\) 半徑為 \(r\) 的圓方程式為 \[ (x-x_1)^2+(y-y_1)^2=r^2 \]過圓上一點的切線方程式
已知一圓圓心為 \(O(a, b)\)，半徑為 \(r\)，圓方程式為 \(C:(x-a)^2+(y-b)^2=r^2\)，假設圓上一點 \(P(x_1, y_1)\)，則過 \(P\) 點且與圓 \(C\) 相切的直線方程式 \(L\) 求法如下：先求 \(\overline{OP}\) 的斜率 \(m_{\overline{OP}}\)。
因為 \(\overline{OP}\perp L\)，所以 \(m_L m_{\overline{OP}}=-1\)，由此求 \(m_L\)。
直線 \(L\) 斜率為 \(m_L\) 且通過點 \(P(x_1, y_1\)，由此求直線 \(L\) 的斜率。
過圓外一點的切線方程式
已知一圓圓心為 \(O(a, b)\)，半徑為 \(r\)，圓方程式為 \(C:(x-a)^2+(y-b)^2=r^2\)，假設圓外一點 \(P(x_1, y_1)\)，則過 \(P\) 點且與圓 \(C\) 相切的直線方程式 \(L\) 求法如下：假設直線 \(L\) 的斜率為 \(m\)，則直線 \(L\) 的方程式為 \(L:y-y_1=m(x-x_1)\)。
利用圓心到直線 \(L\) 的距離為半徑 \(r\)，由此可解出 \(m\)。
除法原理
被除數=除數×商數+餘數除數>餘數
被除式=除式×商式+餘式
deg 除式>deg 餘式
長除法與綜合除法的比較
由下面的過程可以看出長除法跟綜合除法得出的結果相同。長除法 \[ \begin{array}{rrrrrrrrr} & & a_n x^{n-1} & + & (a_{n-1}+ba_n)x^{n-2} & + & [a_{n-2}+b(a_{n-1}+ba_n)]x^{n-3} & + & \cdots \\ \hline x-b & ) & a_nx^n & + & a_{n-1}x^{n-1} & + & a_{n-2}x^{n-2} & + & \cdots \\ & & a_nx^n & - & ba_n x^{n-1} \\ \hline &&&& (a_{n-1}+ba_n)x^{n-1} & + & a_{n-2}x^{n-2} \\ &&&& (a_{n-1}+ba_n)x^{n-1} & - & b(a_{n-1}+ba_n)x^{n-2} \\ \hline &&&&&&[a_{n-2}+b(a_{n-1}+ba_n)]x^{n-2}&+&\cdots \\ \end{array} \]
綜合除法 \[ \begin{array}{rrrrrrrr} a_n & a_{n-1} & a_{n-2} & \cdots & | &b \\ & ba_n & b(a_{n-1}+ba_n) & \cdots & | \\ \hline a_n & (a_{n-1}+ba_n) & [a_{n-2}+b(a_{n-1}+ba_n)] & \cdots \end{array} \]
餘式定理、因式定理
\[ \begin{array}{lcl} f(x)=(ax+b)Q(x)+r &\Leftrightarrow& f\left(\frac{-b}{a}\right)=r, \\ f(x)=(ax+b)Q(x) &\Leftrightarrow& f\left(\frac{-b}{a}\right)=0. \\ \end{array} \]函數圖形的平移
| \(f(x)+1\) | ||||
| ↑ | ||||
| \(f(x+1)\) | ← | \(f(x)\) | → | \(f(x-1)\) |
| ↓ | ||||
| \(f(x)-1\) |
方程式圖形的平移
| \(f(x,y-1)=0\) | ||||
| ↑ | ||||
| \(f(x+1)\) | ← | \(f(x,y)=0\) | → | \(f(x-1)\) |
| ↓ | ||||
| \(f(x,y+1)\) |
二次函數的頂點
二次函數 \(y=f(x)=ax^2+bx+c\) 的頂點 \(x\)-坐標為 \(\frac{-b}{2a}\)三次函數 \(y=f(x)=ax^3+bx^2+cx+d\) 的對稱中心 \(x\)-坐標為 \(\frac{-b}{3a}\)
三次函數圖形的分類
三次函數 \(y=f(x)=ax^3+px\) 的圖形可以分成下面四類。而一般的三次函數 \(y=f(x)=ax^3+bx^2+cx+d\) 都可以經由綜合除法或是配立方法化成形如 \(y=f(x)=a(x-m)^3+p(x-m)+n\) 的樣子。
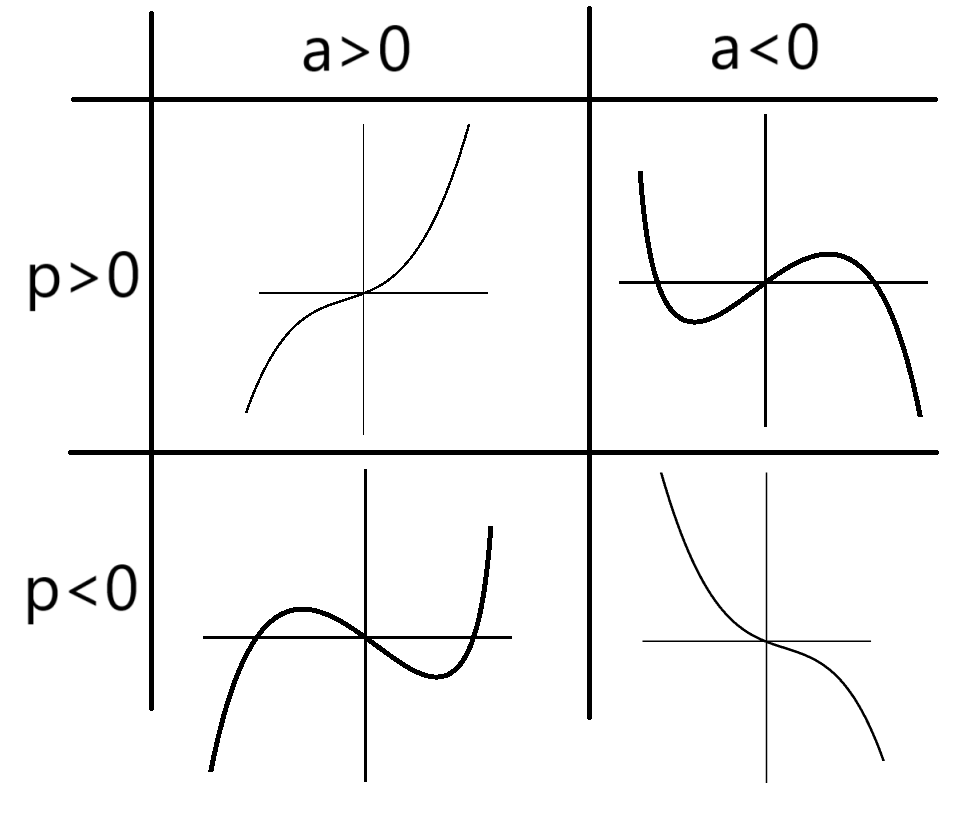
二次函數恆正或恆負
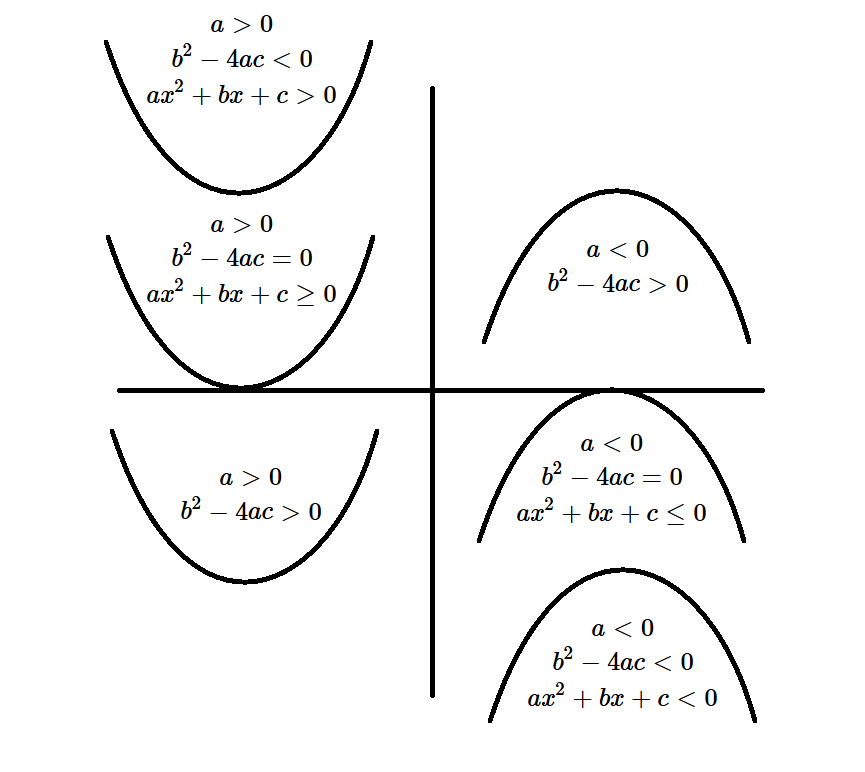
大域特徵與局部特徵
\(y=f(x)=ax^3+bx^2+cx+d\) 在 \(x\) 很大時，\(f(x)\) 的大域特徵近似於 \(ax^3\)。\(y=f(x)=a(x-m)^3+s(x-m)^2+t(x-m)+u\) 在 \(x\) 很靠近 \(m\) 時，\(f(x)\) 的局部特徵近似於 \(y=t(x-m)+u\)。
等差數列、等比數列、等差級數、等比級數
| 數列 | 級數 | |
| 等差 | \(a_1\) \(a_2=a_1+d\), \(a_3=a_1+2d\) \(a_4=a_1+3d\) ... \(a_n=a_1+(n-1)d\) | \(S_n=\frac{(a_1+a_n)n}{2}\) |
| 等比 | \(a_1\) \(a_2=a_1 r\) \(a_3=a_1 r^2\) \(a_4=a_1 r^3\) ... \(a_n=a_1 r^{n-1}\) | \(S_n=\frac{a_1(1-r^{n-1})}{(1-r)}\) |
進階性質
等差數列每n項和又成等差數列等比數列每n項和又成等比數列
\[ \begin{array}{rcllllllllllllllllll} S_n &=& a_1 &+& a_2 &+& a_3 &+& \cdots &+& a_n &=& a_1 &+& (a_1+d) &+& (a_1+2d) &+& \cdots &+& [a_1+(n-1)d] , \\ S_{n+1\sim 2n} &=& a_{n+1} &+& a_{n+2} &+& a_{n+3} &+& \cdots &+& a_{2n} &=& (a_1+nd) &+& [a_1+(n+1)d] &+& [a_1+(n+2)d] &+& \cdots &+& [a_1+(2n-1)d] , \\ S_{2n+1\sim 3n} &=& a_{2n+1} &+& a_{2n+2} &+& a_{2n+3} &+& \cdots &+& a_{3n} &=& (a_1+2nd) &+& [a_1+(2n+1)d] &+& [a_1+(2n+2)d] &+& \cdots &+& [a_1+(3n-1)d] \\ \end{array} \] \[ \begin{array}{rcl} S_n-S_{n+1\sim 2n} &=& nd\times n, \\ S_{2n+1\sim 3n}-S_{n+1\sim 2n} &=& nd\times n \end{array} \] \[ \begin{array}{rcllllllllllllllllll} S_n &=& a_1 &+& a_2 &+& a_3 &+& \cdots &+& a_n &=& a_1 &+& a_1 r &+& a_1 r^2 &+& \cdots &+& a_1 r^{n-1} , \\ S_{n+1\sim 2n} &=& a_{n+1} &+& a_{n+2} &+& a_{n+3} &+& \cdots &+& a_{2n} &=& a_1 r^n &+& a_1 r^{n+1} &+& a_1 r^{n+2} &+& \cdots &+& a_1 r^{2n-1} , \\ S_{2n+1\sim 3n} &=& a_{2n+1} &+& a_{2n+2} &+& a_{2n+3} &+& \cdots &+& a_{3n} &=& a_1 r^{2n} &+& a_1 r^{2n+1} &+& a_1 r^{2n+2} &+& \cdots &+& a_1 r^{3n-1} \\ \end{array} \] \[ \begin{array}{rcl} S_n÷S_{n+1\sim 2n} &=& r^n, \\ S_{2n+1\sim 3n}÷S_{n+1\sim 2n} &=& r^n \end{array} \]
平方和公式、立方和公式
\[ \begin{array}{ccl} 1+2+\cdots+n &=& \frac{n(n+1)}{2}, \\ 1^2+2^2+\cdots+n^2 &=& \frac{1}{6}n(n+1)(2n+1), \\ 1^3+2^3+\cdots+n^3 &=& \left[\frac{n(n+1)}{2}\right]^2. \end{array} \]排容原理
\[ \begin{array}{rcl} n(A\cup B\cup C) &=& n(A)+n(B)+n(C) \\ && -n(A\cap B)-n(B\cap C)-n(A\cap C) \\ && +n(A\cap B\cap C). \end{array} \] 最簡單最直覺的證明
排列組合
\(P^n_r\) 表示n個東西取r個"排列"的方法數\(C^n_r\) 表示n個東西取r個"不排列"的方法數 \[ P^n_r=\frac{n!}{(n-r)!} \] 筆者的背法是，寫 \(n\)，然後往下寫階乘 \(r\) 個（包括 \(n\) 總共 \(r\) 個），例如 \(P^{7}_{3}=7\times 6\times 5\)。 \[ C^n_r=\frac{n!}{r!(n-r)!} \] 筆者的背法是，寫 \(n\)，然後往下寫階乘 \(r\) 個（包括 \(n\) 總共 \(r\) 個），再除以 \(r!\)，例如 \(C^{7}_{3}=\frac{7\times 6\times 5}{3\times 2\times 1}\)。
巴斯卡定理
| n | n+1 | ||
| r | \(C^n_r\) | ||
| + | |||
| r+1 | \(C^n_{r+1}\) | = | \(C^{n+1}_{r+1}\) |
\(C^n_r+C^n_{r+1}=C^{n+1}_{r+1}\)，上標為行，下標為列，注意到按照此編號排序，加的規則變成：上加下等於右下，一個L型。
所以這題 \(C^{10}_{5}+C^{10}_{6}+C^{11}_{7}+C^{12}_{8}\) 可以用如下的表格來幫助計算並完成。| 10 | 11 | 12 | 13 | |
| 5 | \(C^{10}_{5}\) | |||
| 6 | \(C^{10}_{6}\) | |||
| 7 | \(C^{11}_{7}\) | |||
| 8 | \(C^{12}_{8}\) |
二項式定理
\[ (x+y)^n=C^n_n x^n+C^n_{n-1}x^{n-1}y+C^n_{n-2}x^{n-2}y^2+\cdots +C^n_2 x^2y^{n-2}+C^n_1 xy^{n-1}+C^n_0 y^n \]數據平移與伸縮對各統計量的影響
| 數據 | \(+a\) | \(\times k\) |
| 均眾中 | \(+a\) | \(\times k\) |
| 差距 | 不變 | \(\times |k|\) |
均中眾表示算術平均數、中位數、眾數，差距表示標準差、全距。
用數學符號來表示，就是
\(\mu_{ax+b}=a\mu_x+b\)\(\mu_{cy+d}=c\mu_y+d\)
\(\sigma_{ax+b}=|a|\sigma_x\)
\(\sigma_{cy+d}=|c|\sigma_y\)
類似的，在二維數據也有類似的結果。
\(S_{ax+b, ax+b}=a^2S_{xx}\)\(S_{cy+d, cy+d}=c^2S_{yy}\)
\(S_{ax+b,cy+d}=acS_{xy}\)
\(r_{ax+b,cy+d}=\frac{ac}{|ac|}r_{x,y}\)
標準差、離均平方差、數據平方和
一維數據二維數據 \[ \begin{array}{rcl} S_{xy} &=& (x_1-\mu_x)(y_1-\mu_y)+(x_2-\mu_x)(y_2-\mu_y)+\cdots+(x_n-\mu_x)(y_n-\mu_y) \\ &=& (x_1 y_1+x_2 y_2+\cdots+x_n y_n)-n\mu_x \mu_y \end{array} \]
數據更新標準差（這個不好用，直接用 \(x_1^2+x_2^2+\cdots=n_{\text{old}}(\mu_{\text{old}}^2+\sigma_{\text{old}}^2)\)，來推 \(x_1^2+x_2^2+\cdots=n_{\text{new}}(\mu_{\text{new}}^2+\sigma_{\text{new}}^2)\)）
| 舊數據 | 平移前 | 平移後 | 新數據 | 平移前 | 平移後 | |
| μ_old | ① | ④ | μ_new | ③ | ⑦ | |
| σ_old | ② | ⑤ | σ_new | X | ⑨ | |
| Σx²_old | X | ⑥ | Σx²_new | X | ⑧ |
數據合併標準差
| 第一組x | 平移前 | 平移後 | 第二組y | 平移前 | 平移後 | 全體 | 平移前 | 平移後 | ||
| μ_x | ① | ⑥ | μ_y | ③ | ⑨ | μ_all | ⑤ | ⑫ | ||
| σ_x | ② | ⑦ | σ_y | ④ | ⑩ | σ_all | X | ⑭ | ||
| Σx² | X | ⑧ | Σy² | X | ⑪ | Σx²+y² | X | ⑬ |
相關係數與迴歸直線
相關係數\(r=\frac{S_{xy}}{\sqrt{S_{xx}}\sqrt{S_{yy}}}\)
\(r=\frac{S_{xy}}{\sqrt{n}\sigma_x \sqrt{n}\sigma_y}\)
回歸直線
\(y-\mu_y=\frac{S_{xy}}{S_{xx}}(x-\mu_x)\)
\(y-\mu_y=r\frac{\sigma_y}{\sigma_x}(x-\mu_x)\)
用表格來算
| \(x_i\) | \(y_i\) | \(x_i-\mu_x\) | \(y_i-\mu_y\) | \((x_i-\mu_x)(y_i-\mu_y)\) | \((x_i-\mu_x)^2\) | \((y_i-\mu_y)^2\) |
| \(\vdots\) | \(\vdots\) | \(\vdots\) | \(\vdots\) | \(\vdots\) | \(\vdots\) | \(\vdots\) |
| 用來算 \(\mu_x\) | 用來算 \(\mu_y\) | 0 | 0 | \(S_{xy}\) | \(S_{xx}\) | \(S_{yy}\) |
圓周長與弧長、圓面積與扇形面積
| 圓 | 全部 | 部分 |
| 長度 | 圓周長\(=2r\pi\) | 弧長\(=2r\pi\frac{\theta}{2\pi}\) |
| 面積 | 圓面積\(=r^2\pi\) | 扇形面積\(=r^2\pi\frac{\theta}{2\pi}\) |
三角函數
|
\(\sin{\theta}=\frac{對邊}{斜邊}\) \(\cos{\theta}=\frac{鄰邊}{斜邊}\) \(\tan{\theta}=\frac{對邊}{鄰邊}\) |
|
\(\sin^2{\theta}+\cos^2{\theta}=1\) \(\tan{\theta}=\frac{\sin{\theta}}{\cos{\theta}}\) \(\sin{(90^{\circ}-\square)}=\cos{\square}\) \(\cos{(90^{\circ}-\square)}=\sin{\square}\) | ||||||||||||||||||||||||||||||||||||
|
\(\sin{\theta}=\frac{y}{r}\) \(\cos{\theta}=\frac{x}{r}\) \(\tan{\theta}=\frac{y}{x}\) |
|
|
正弦定理、餘弦定理
| 正弦定理 \(\frac{a}{\sin{A}}=\frac{b}{\sin{B}}=\frac{c}{\sin{C}}=2R\) 其中 \(R\) 為外接圓半徑 | 三角形面積公式 (1). \(\frac{1}{2}ab\sin{C}\) (2). \(\sqrt{s(s-a)(s-b)(s-c)}\) 其中 \(s\) 為半周長 \(\frac{a+b+c}{2}\) (3). \(rs\) 其中 \(r\) 為內切圓半徑 (4). \(\frac{abc}{4R}\) | 分角線長度公式 \(AD^2=AB\times AC-BD\times DC\) |
| 餘弦定理 \(c^2=a^2+b^2-2ab\cos{C}\) \(\cos{C}=\frac{a^2+b^2-c^2}{2ab}\) | 四邊形面積公式 \(\frac{1}{2}(a+b)(c+d)\sin{\theta}\) | 中線長度公式 \(AB^2+AC^2=2(AM^2+BM^2)\) |
和角公式
\[ \begin{array}{rcl} \sin{(A+B)} &=& \sin{A}\cos{B}+\sin{B}\cos{A} \\ \sin{(A-B)} &=& \sin{A}\cos{B}-\sin{B}\cos{A} \\ \cos{(A+B)} &=& \cos{A}\cos{B}-\sin{A}\sin{B} \\ \cos{(A-B)} &=& \cos{A}\cos{B}+\sin{A}\sin{B} \\ \tan{(A+B)} &=& \frac{\tan{A}+\tan{B}}{1-\tan{A}\tan{B}} \\ \tan{(A-B)} &=& \frac{\tan{A}-\tan{B}}{1+\tan{A}\tan{B}} \end{array} \] \[ \begin{array}{rcl} \sin{2\theta} &=& 2\sin{\theta}\cos{\theta} \\ \cos{2\theta} &=& \cos^2{\theta}-\sin^2{\theta}=1-2\sin^2{\theta}=2\cos^2{\theta}-1 \\ \tan{2\theta} &=& \frac{2\tan{\theta}}{1-\tan^2{\theta}} \end{array} \] \[ \begin{array}{rcl} \sin{\frac{\theta}{2}} &=& \pm\sqrt{\frac{1-\cos{\theta}}{2}} \\ \cos{\frac{\theta}{2}} &=& \pm\sqrt{\frac{1+\cos{\theta}}{2}} \\ \tan{\frac{\theta}{2}} &=& \frac{\sin{\theta}}{1+\cos{\theta}} \end{array} \] \[ \begin{array}{rcl} *\sin{2\theta} &=& \frac{2\tan{\theta}}{1+\tan^2{\theta}} \\ *\cos{2\theta} &=& \frac{1-\tan^2{\theta}}{1+\tan^2{\theta}} \end{array} \]函數圖形的伸縮
*To graph \(y=2f(x)\), stretch the graph of \(y=f(x)\) vertically by a factor of \(2\).To graph \(y=\frac{1}{2}f(x)\), shrink the graph of \(y=f(x)\) vertically by a factor of \(\frac{1}{2}\).
To graph \(y=f(2x)\), shrink the graph of \(y=f(x)\) horizontally by a factor of \(\frac{1}{2}\).
*To graph \(y=f(\frac{1}{2}x)\), stretch the graph of \(y=f(x)\) horizontally by a factor of \(2\).
分點公式
\[ \vec{PC}=\frac{n}{m+n}\vec{PA}+\frac{m}{m+n}\vec{PB} \]共線定理
三角形的四心，向量版
\(I\) 為 \(\triangle ABC\) 的內心，\(P\) 為任一點，則 \[ \vec{PI}=\frac{a}{a+b+c}\vec{PA}+\frac{b}{a+b+c}\vec{PB}+\frac{c}{a+b+c}\vec{PC}. \] \(G\) 為 \(\triangle ABC\) 的重心，\(P\) 為任一點，則 \[ \vec{PG}=\frac{1}{3}\vec{PA}+\frac{1}{3}\vec{PB}+\frac{1}{3}\vec{PC}. \] \(O\) 為 \(\triangle ABC\) 的外心，則 \[ \vec{AO}\cdot \vec{AB}=\frac{1}{2}\overline{AB}^2. \] \(H\) 為 \(\triangle ABC\) 的垂心，則 \[ \vec{AH}\cdot \vec{AB}=\vec{AB}\cdot \vec{AC}. \]正射影
向量 \(\vec{a}\) 在向量 \(\vec{b}\) 上的正射影為 \[ \vec{p}=\frac{\vec{a}\cdot \vec{b}}{|\vec{b}|^2}\vec{b} \]柯西不等式
\[ (\square^2+\diamond^2)(\triangle^2+\circ^2)\geq (\square \triangle+\diamond \circ)^2 \]方向向量，法向量
| \(ax+by+c=0\) | \(x=dt+e\) \(y=ft+g\) | |
| 方向向量 | 法向量的 \(x, y\) 互換，其中一個變號 | \((d, f)\) ↓ |
| 法向量 | ↑ \((a, b)\) | 方向向量的 \(x, y\) 互換，其中一個變號 |
二階行列式、三階行列式、內積、外積
| 二階行列式 | 三階行列式 | 內積 | 外積 | |
| 定義與性質 | \(\vec{a}=(x_1, y_1)\) \(\vec{b}=(x_2, y_2)\) \(\det{\begin{bmatrix}x_1&y_1\\ x_2&y_2\end{bmatrix}}=x_1y_2-x_2y_1\) |
\(\vec{a}=(x_1, y_1, z_1)\) \(\vec{b}=(x_2, y_2, z_2)\) \(\vec{c}=(x_3, y_3, z_3)\) \(\det{\begin{bmatrix}x_1&y_1&z_1\\x_2&y_2&z_2\\ x_3&y_3&z_3\end{bmatrix}}\) \(=x_1y_2z_3+x_2y_3z_1+x_3y_1z_2-z_1y_2x_3-z_2y_3x_1-z_3y_1x_2\) \(=x_1\det{\begin{bmatrix}y_2&z_2\\y_3&z_3\end{bmatrix}}-x_2\det{\begin{bmatrix}y_1&z_1\\ y_3&z_3\end{bmatrix}}+x_3\det{\begin{bmatrix}y_1&z_1\\y_2&z_2\end{bmatrix}}\) \(=\vec{a}\cdot(\vec{b}\times \vec{c})\) |
\(\vec{a}=(x_1, y_1)\) \(\vec{b}=(x_2, y_2)\) \(\vec{a}\cdot \vec{b}\) \(=|\vec{a}|\cdot |\vec{b}|\cdot \cos{\theta}\) \(=x_1x_2+y_1y_2\) \(\vec{a}=(x_1, y_1, z_1)\) \(\vec{b}=(x_2, y_2, z_2)\) \(\vec{a}\cdot \vec{b}=x_1x_2+y_1y_2+z_1z_2\) |
\(\vec{a}=(x_1, y_1, z_1)\) \(\vec{b}=(x_2, y_2, z_2)\) \(\vec{a}\times \vec{b}=\det{\begin{bmatrix}\vec{i}&\vec{j}&\vec{k}\\x_1&y_1&z_1\\ x_2&y_2&z_2\end{bmatrix}}\) |
| 幾何意義 | 向量 \(\vec{a}, \vec{b}\) 決定的平行四邊形面積為 \(|\det{\begin{bmatrix}x_1&y_1\\ x_2&y_2\end{bmatrix}}|\)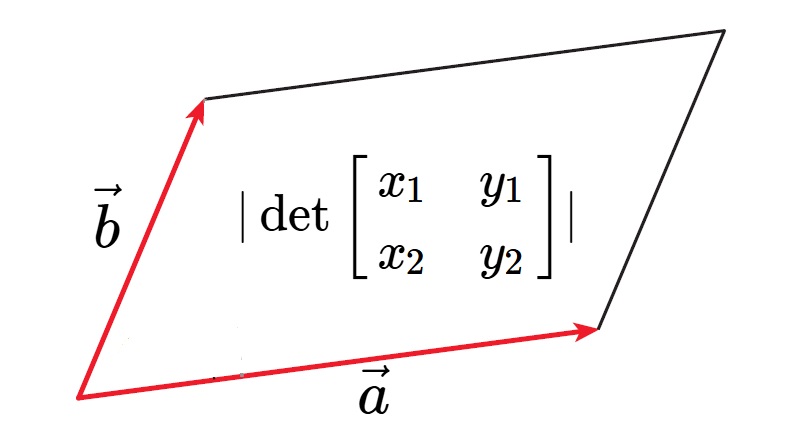 | 向量 \(\vec{a}, \vec{b}, \vec{c}\) 決定的平行六面體體積為 \(|\det{\begin{bmatrix}x_1&y_1&z_1\\ x_2&y_2&z_2\\x_3&y_3&z_3\end{bmatrix}}|\)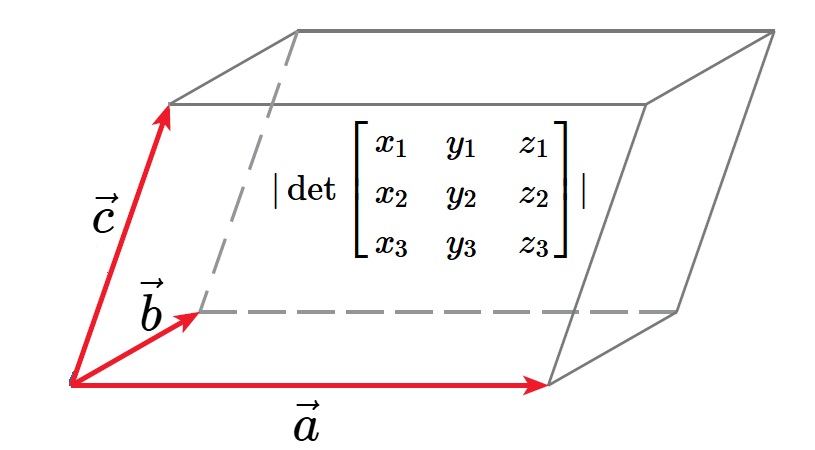 | \(W=\vec{F}\cdot \vec{s}\)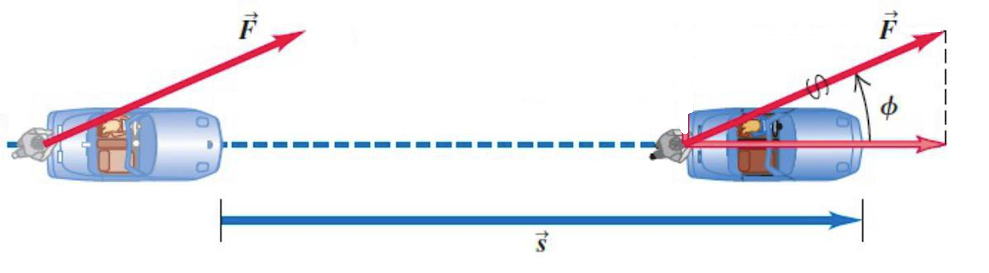 | \(|\vec{a}\times \vec{b}|=|\vec{a}|\cdot |\vec{b}|\cdot \sin{\theta}\) |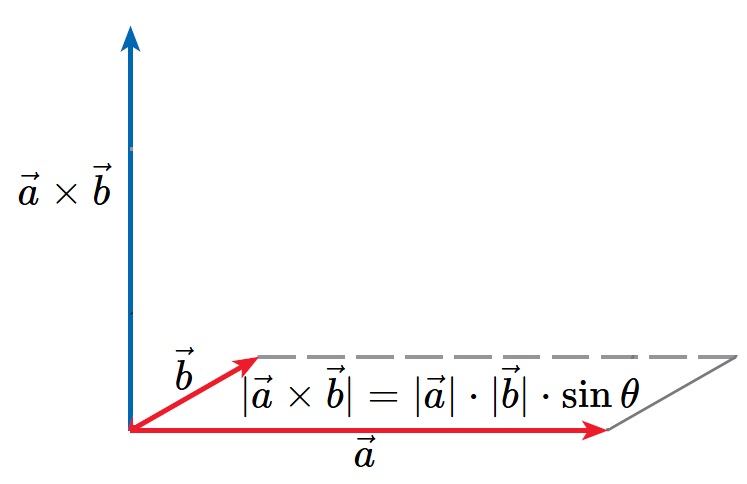
容易混淆的部分
- \(\vec{a}\cdot \vec{b}\) 為純量，\(\vec{a}\times \vec{b}\) 為向量。
- 平行六面體體積為 \(\det{\begin{bmatrix}x_1&y_1&z_1\\ x_2&y_2&z_2\\ x_3&y_3&z_3\end{bmatrix}}\)，外積定義為 \(\vec{a}\times \vec{b}=\det{\begin{bmatrix}\vec{i}&\vec{j}&\vec{k}\\ x_1&y_1&z_1\\ x_2&y_2&z_2\end{bmatrix}}\)
- \(\vec{a}\cdot \vec{b}=|\vec{a}|\cdot |\vec{b}|\cdot \cos{\theta}\)，\(|\vec{a}\times \vec{b}|=|\vec{a}|\cdot |\vec{b}|\cdot \sin{\theta}\)
- 平面上 \((x_1, y_1), (x_2, y_2), (x_3, y_3)\) 三點圍成的三角形面積為 \(\frac{1}{2}|\det{\begin{bmatrix}x_1&y_1&1\\ x_2&y_2&1\\x_3&y_3&1\end{bmatrix}}|\)
- 平面上三線 \(\left\{\begin{array}{rcl}a_1x+b_1y=c_1\\a_2x+b_2y=c_2\\a_3x+b_3y=c_3\end{array}\right.\) 共點，則 \(\det{\begin{bmatrix}a_1&b_1&c_1\\a_2&b_2&c_2\\a_3&b_3&c_3\end{bmatrix}}=0\)
- 空間中三向量決定的四面體體積為六面體體積的 \(\frac{1}{6}\) 倍。
點線面之間的距離
| 點 | 線 | 面 | |
| 點 | 兩點距（平面） \(\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}\) 兩點距（空間） \(\sqrt{(x_1-x_2)^2+(y_1-y_2)^2+(z_1-z_2)^2}\) |
||
| 線 | 點線距（平面） \(\frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}\) *點線距（空間） |
兩線距（平面） \(\frac{|c_1-c_2|}{\sqrt{a^2+b^2}}\) *兩線距（空間） |
|
| 面 | 點面距 \(\frac{|ax_0+by_0+cz_0+d|}{\sqrt{a^2+b^2+c^2}}\) |
面線距 | 兩面距 \(\frac{|d_1-d_2|}{\sqrt{a^2+b^2+c^2}}\) |
點法式、參數式
平面上的直線 點法式 \(p(x-x_0)+q(y-y_0)=0\) | 空間中的平面 點法式 \(p(x-x_0)+q(y-y_0)+r(z-z_0)=0\) |
平面上的直線 參數式 \(\left\{\begin{array}{l}x=x_0+ta\\y=y_0+tb\end{array}\right.\) | 空間中的直線 參數式 \(\left\{\begin{array}{l}x=x_0+ta\\y=y_0+tb\\z=z_0+tc\end{array}\right.\) |
系
| 直線系 | 圓系 | 平面系 |
| \(L_1:a_1x+b_1y+c_1=0\) \(L_2:a_2x+b_2y+c_2=0\) \(L_1\cap L_2=P\) 通過 \(P\) 的直線可設為 \((a_1x+b_1y+c_1)+k(a_2x+b_2y+c_2)=0\) | \(C_1:x^2+a_1x+y^2+b_1y+c_1=0\) \(C_2:x^2+a_2x+y^2+b_2y+c_2=0\) \(C_1\cap C_2=P, Q\) 通過 \(P, Q\) 的圓可設為 \((x^2+a_1x+y^2+b_1y+c_1)+k(x^2+a_2x+y^2+b_2y+c_2)=0\) | \(E_1:a_1x+b_1y+c_1z+d_1=0\) \(E_2:a_2x+b_2y+c_2z+d_2=0\) \(E_1\cap E_2=L\) 通過 \(L\) 的平面可設為 \((a_1x+b_1y+c_1z+d_1)+k(a_2x+b_2y+c_2z+d_2)=0\) |
No comments:
Post a Comment