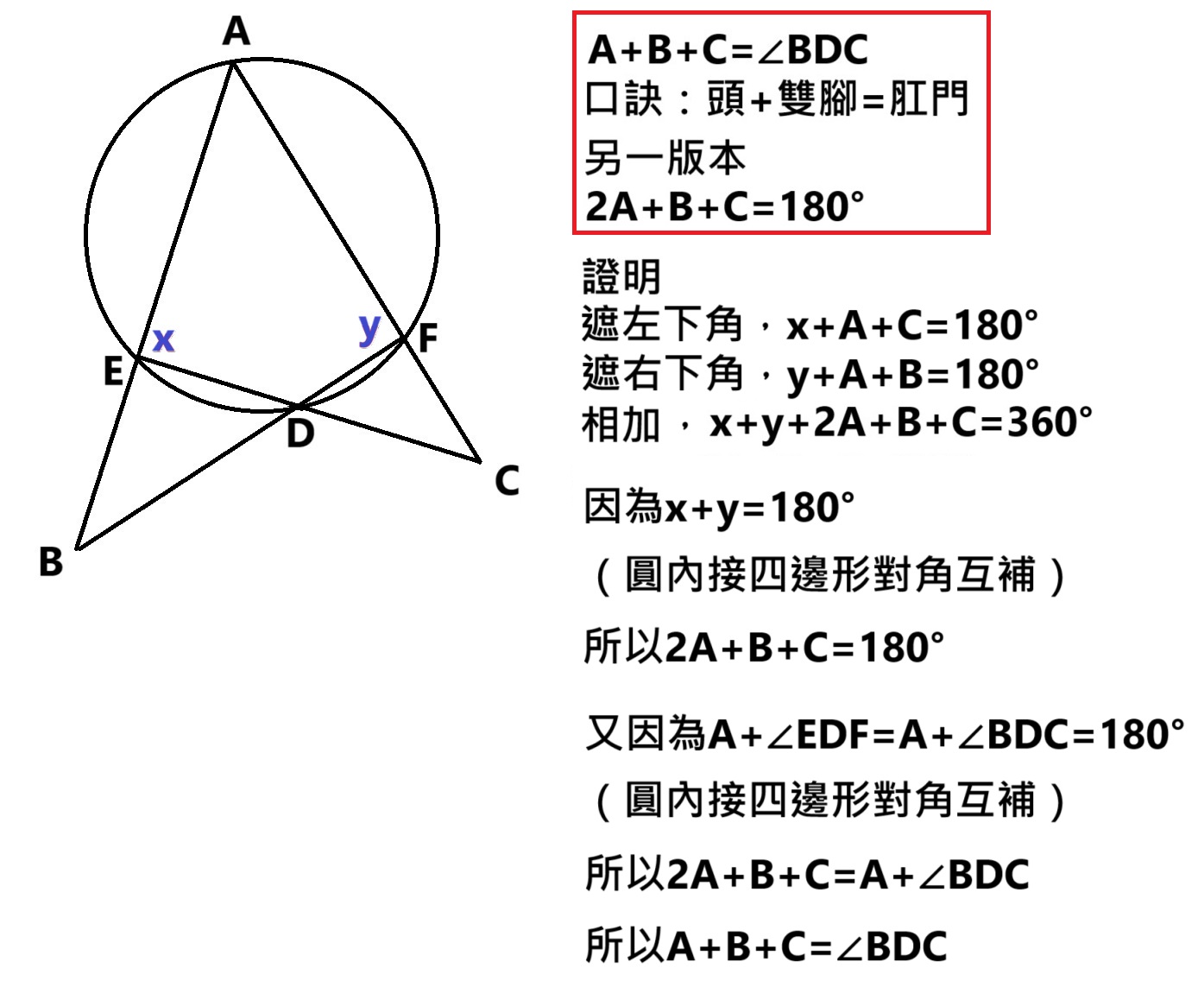
正四面體中 \[ \frac{\text{邊長}}{\text{高}}=\frac{\sqrt{6}}{2}, \cos{\text{面與面的夾角}}=\frac{1}{3}, \cos{\text{邊與面的夾角}}=\frac{1}{\sqrt{3}}, \]
zometool龍圖兒，官方網站賣31美金，運費也要31美金，很貴。
遊思樂頂點珠造型棒USL Geometric Construction Set 這套玩具包含數個圓球與直棍，直棍的長短不一，圓球上的孔洞如這個圖形所示，沒辦法製作出正四面體。各孔洞的座標可以用Spherical Coordinates算出來（參考Calculus課本），然後孔洞跟孔洞之間的夾角，可以用Mathematica的
VectorAngle算出來，就可以知道能不能製作出想要的形體。
北模113數學第二次17
設 \(f(x)\) 與 \(g(x)\) 皆為實係數二次多項式且首項係數都是 \(1\)，已知 \((f(x))^2\) 除以 \(g(x)\) 的餘式為 \(2x+1\)，而 \((g(x))^2\) 除以 \(f(x)\) 的餘式為 \(x+1\)，則 \(f(x)+g(x)\) Ans: \(2x^2-3x-2\)這題是出自雙週一題103學年度第二學期第一題
| \(\vec{v}=(x_1, y_1)\) \(\vec{w}=(x_2, y_2)\) | 幾何 | 代數 |
| \(\vec{v}+\vec{w}\) | \(\vec{v}+\vec{w}=(x_1+x_2, y_1+y_2)\) | |
| \(\vec{v}-\vec{w}\) | \(\vec{v}-\vec{w}=(x_1-x_2, y_1-y_2)\) | |
| \(a\vec{v}\) | \(a\vec{v}=(ax_1, ay_1)\) | |
| \(\vec{v}\cdot\vec{w}\) | \(\vec{v}\cdot \vec{w}=(x_1\cdot x_2, y_1\cdot y_2)\) | |
| \((a\vec{v}+b\vec{w})\cdot (c\vec{p}+d\vec{r})\) | ||
| \(|\vec{v}|\) | \(|\vec{v}|=\sqrt{x_1^2+y_1^2}\) | |
| \(|\vec{v}|^2=\vec{v}\cdot \vec{v}\) | ||
| \(\vec{v}\parallel\vec{w}\) | \(\vec{v}=t\vec{w}\) | |
| \(\vec{v}\perp\vec{w}\) | \(\vec{v}\cdot \vec{w}=0\) | |
| 分點公式 | \(\vec{PC}=\frac{m}{m+n}\vec{PA}+\frac{n}{m+n}\vec{PB}\) | |
| 共線定理 | 已知 \(\vec{PC}=s\vec{PA}+t\vec{PB}\) \(A, B, C\) 共線 \(\Leftrightarrow\) \(s+t=1\) | |
| 柯西不等式 | \((x_1^2+y_1^2)(x_2^2+y_2^2)\geq (x_1 x_2+y_1 y_2)^2\) \(|\vec{v}|^2 |\vec{w}|^2\geq (\vec{v}\cdot \vec{w})^2\) | |
| 正射影 | \(\text{proj}_{\vec{w}}\vec{w}=\frac{\vec{v}\cdot \vec{w}}{|\vec{w}|^2}\vec{w}\) | |
| 正射影長度 | \(|\text{proj}_{\vec{w}}\vec{w}|=\frac{|\vec{v}\cdot \vec{w}|}{|\vec{w}|}\) | |
| 夾角 | \(\cos{\theta}=\frac{\vec{v}\cdot \vec{w}}{|\vec{v}|\cdot |\vec{w}|}\) | |
| 三角形面積 | \(\frac{1}{2}\sqrt{|\vec{v}|^2|\vec{w}|^2-(\vec{v}\cdot\vec{w})^2}\) \(|\det{\begin{bmatrix}x_1&y_1\\x_2&y_2\end{bmatrix}}|\) | |
| 克拉瑪法則 | \(\left\{\begin{array}{rcl}a_1x+b_1y&=&c_1\\a_2x+b_2y&=&c_2\\\end{array}\right.\) \(x=\frac{\Delta_x}{\Delta}=\frac{\det{\begin{bmatrix}a_1&b_1\\a_2&b_2\end{bmatrix}}}{\det{\begin{bmatrix}c_1&b_1\\c_2&b_2\end{bmatrix}}}\) \(y=\frac{\Delta_y}{\Delta}=\frac{\det{\begin{bmatrix}a_1&c_1\\a_2&c_2\end{bmatrix}}}{\det{\begin{bmatrix}c_1&b_1\\c_2&b_2\end{bmatrix}}}\) | |
| 行列式的定義 | \(\det{\begin{bmatrix}a&b\\c&d\end{bmatrix}}=ad-bc\) | |
| 行列式的性質 | \(\det{\begin{bmatrix}ka&kb\\c&d\end{bmatrix}}=k\cdot \det{\begin{bmatrix}a&b\\c&d\end{bmatrix}}\) | |
| 行列式的性質 | \(\det{\begin{bmatrix}a&b\\c+ka&d+kb\end{bmatrix}}=\det{\begin{bmatrix}a&b\\c&d\end{bmatrix}}\) | |
| 行列式的性質 | \(\det{\begin{bmatrix}a&b\\c+e&d+f\end{bmatrix}}=\det{\begin{bmatrix}a&b\\c&d\end{bmatrix}}+\det{\begin{bmatrix}a&b\\e&f\end{bmatrix}}\) | |
| 行列式的性質 | \(\det{\begin{bmatrix}c&d\\a&b\end{bmatrix}}=(-1)\cdot \det{\begin{bmatrix}a&b\\c&d\end{bmatrix}}\) | |
| 行列式的性質 | \(\det{\begin{bmatrix}a&c\\b&d\end{bmatrix}}=\det{\begin{bmatrix}a&b\\c&d\end{bmatrix}}\) | |
| 內心 | \(\vec{PI}=\frac{a}{a+b+c}\vec{PA}+\frac{b}{a+b+c}\vec{PB}+\frac{c}{a+b+c}\vec{PC}\) | |
| 重心 | \(\vec{PG}=\frac{1}{3}\vec{PA}+\frac{1}{3}\vec{PB}+\frac{1}{3}\vec{PC}\) \(\vec{AG}=\frac{1}{3}\vec{AB}+\frac{1}{3}\vec{AC}\) \(\vec{0}=\vec{GA}+\vec{GB}+\vec{GC}\) | |
| 外心 | \(\vec{AB}\cdot \vec{AO}=\frac{1}{2}|\vec{AB}|^2\) | |
| 垂心 | \(\vec{AB}\cdot \vec{AH}=\vec{AB}\cdot \vec{AC}\) |
If \(P(x)\) is a polynomial with real coefficients, written with descending powers of \(x\) (and omitting powers with coefficient \(0\)), then a variation in sign occurs whenever adjacent coefficients have opposite signs.
Descartes's Rule of Signs
Let \(P\) be a polynomial with real coefficients.
1. The number of positive real zeros of \(P(x)\) either is equal to the number of variations in sign in \(P(x)\) or is less than that by an even whole number.
2. The number of negative real zeros of \(P(x)\) either is equal to the number of variations in sign in \(P(-x)\) or is less than that by an even whole number.
We say that \(a\) is a lower bound and \(b\) is an upper bound for the zeros of a polynomial if every real zero \(c\) of the polynomial satisfies \(a\leq c\leq b\).
The Upper and Lower Bounds Theorem
Let \(P\) be a polynomial with real coefficient.
1. If we divide \(P(x)\) by \(x-b\) (with \(b\gt 0\)) using synthetic division and if the row that contains the quotient and remainder has no negative entry, then \(b\) is an upper bound for the real zeros of \(P\).
2. If we divide \(P(x)\) by \(x-a\) (with \(a\lt 0\)) using synthetic division and if the row that contains the quotient and remainder has entries that are alternately nonpositive and nonnegative, then \(a\) is a lower bound for the real zeros of \(P\).
| 函數 | \(y=x\) | \(y=x^2\) |
| 圖形 | ||
| 函數 | \(y=ax^3+px\) | \(y=\sqrt{x}\) |
| 圖形 | ||
| 函數 | \(y=2^x\) | \(y=\left(\frac{1}{2}\right)^x\) |
| 圖形 | ||
| 函數 | \(y=\log_2{x}\) | \(y=\log_{\frac{1}{2}}{x}\) |
| 圖形 |
| 函數 | \(y=\sin{x}\) | \(y=\cos{x}\) | \(y=\tan{x}\) |
| 圖形 |
不換
|
1 |
2 | 3 | 4 | 5 | ||||
| 🚗 | 🐐 | 🐐 | 🐐 | 🐐 | 一開始選2 | 主持人開4, 5 | 不換 | 結果Lose |
| 🐐 | 🚗 | 🐐 | 🐐 | 🐐 | 一開始選2 | 主持人開4, 5 | 不換 | 結果Win |
| 🐐 | 🐐 | 🚗 | 🐐 | 🐐 | 一開始選2 | 主持人開4, 5 | 不換 | 結果Lose |
| 🐐 | 🐐 | 🐐 | 🚗 | 🐐 | 一開始選2 | 主持人開3, 5 | 不換 | 結果Lose |
| 🐐 | 🐐 | 🐐 | 🐐 | 🚗 | 一開始選2 | 主持人開3, 4 | 不換 | 結果Lose |
換門
|
1 |
2 | 3 | 4 | 5 | ||||
| 🚗 | 🐐 | 🐐 | 🐐 | 🐐 | 一開始選2 | 主持人開4, 5 | 從2換成1 | 結果Win |
| 🚗 | 🐐 | 🐐 | 🐐 | 🐐 | 一開始選2 | 主持人開4, 5 | 從2換成3 | 結果Lose |
| 🐐 | 🚗 | 🐐 | 🐐 | 🐐 | 一開始選2 | 主持人開4, 5 | 從2換成1 | 結果Lose |
| 🐐 | 🚗 | 🐐 | 🐐 | 🐐 | 一開始選2 | 主持人開4, 5 | 從2換成3 | 結果Lose |
| 🐐 | 🐐 | 🚗 | 🐐 | 🐐 | 一開始選2 | 主持人開4, 5 | 從2換成1 | 結果Lose |
| 🐐 | 🐐 | 🚗 | 🐐 | 🐐 | 一開始選2 | 主持人開4, 5 | 從2換成3 | 結果Win |
| 🐐 | 🐐 | 🐐 | 🚗 | 🐐 | 一開始選2 | 主持人開3, 5 | 從2換成1 | 結果Lose |
| 🐐 | 🐐 | 🐐 | 🚗 | 🐐 | 一開始選2 | 主持人開3, 5 | 從2換成4 | 結果Win |
| 🐐 | 🐐 | 🐐 | 🐐 | 🚗 | 一開始選2 | 主持人開3, 4 | 從2換成1 | 結果Lose |
| 🐐 | 🐐 | 🐐 | 🐐 | 🚗 | 一開始選2 | 主持人開3, 4 | 從2換成5 | 結果Win |
正確但有瑕疵
|
1 |
2 | 3 | ||||
| 🚗 | 🐐 | 🐐 | 一開始選1 | 主持人開3 | 從1換成2 | 結果Lose |
| 🐐 | 🚗 | 🐐 | 一開始選1 | 主持人開3 | 從1換成2 | 結果Win |
| 🐐 | 🐐 | 🚗 | 一開始選1 | 主持人開2 | 從1換成3 | 結果Win |
常見誤解：主持人開哪一扇門沒有差別，主持人開的門不固定，參賽者更換的門不固定
不正確但無瑕疵
|
1 |
2 | 3 | ||||
| 🚗 | 🐐 | 🐐 | 一開始選1 | 主持人開3 | 從1換成2 | 結果Lose |
| 🚗 | 🐐 | 🐐 | 一開始選1 | 主持人開2 | 從1換成3 | 結果Lose |
| 🐐 | 🚗 | 🐐 | 一開始選1 | 主持人開3 | 從1換成2 | 結果Win |
| 🐐 | 🐐 | 🚗 | 一開始選1 | 主持人開2 | 從1換成3 | 結果Win |
為了考察某校各班學生參加週末清淨校園活動的人數，在全校隨機抽取4個班級，並把這4個班級參加此活動的學生人數作為資料數據。已知該筆數據的平均數為7人，中位數為k人，標準差為1人，則k之值為Ans: 7
由標準差為1，得到 \((x_1-7)^2+(x_2-7)^2+(x_3-7)^2+(x_4-7)^2=4\)，因為 \(x_1, x_2, x_3, x_4\) 皆為整數，所以上述各項皆為 \(0\) 或 \(1\) 或 \(4\)。
上述各項中有一項為 \(4\) \[ \begin{array}{rl} \Rightarrow & (x_4-7)^2=4 \text{ or }(x_1-7)^2=4 \\ \Rightarrow & x_4=9 \text{ or }x_1=5 \\ \Rightarrow & x_4=9, x_1=x_2=x_3=7 \text{ or }x_1=5, x_2=x_3=x_4=7 \\ \Rightarrow & \mu=10\neq 7 \text{ or } \mu=\frac{26}{4}\neq 7 \end{array} \]
上述各項皆為 \(1\)，則 \(x_1, x_2, x_3, x_4\) 等於 \(6\) 或 \(8\)，只有 \(x_1=x_2=6, x_3=x_4=8\) 滿足 \(\mu=7\)。
\[y=af(k(x-d))+c\] mapping notation \[(x,y)\to (\frac{x}{k}+d, ay+c)\] 原圖形對稱於原點
⇒v在原圖形上且-v在原圖形上
⇒T(v)在新圖形上且T(-v)在新圖形上
⇒T(v)在新圖形上且-T(v)在新圖形上
⇒變換後的新圖形對稱於原點
\[ \sin{15^{\circ}}=\cos{75^{\circ}}=\frac{\sqrt{6}-\sqrt{2}}{4} \] \[ \cos{15^{\circ}}=\sin{75^{\circ}}=\frac{\sqrt{6}+\sqrt{2}}{4} \] 一副樸克牌有52張，分為四種花色：黑桃、紅心、方塊、梅花，每種花色有13張牌，今有4人玩橋牌，每人各拿13張牌，若南家與北家共有9張紅心，則東、西兩家各有2張紅心的機率是Ans:234/575（未解決）
| 1 | 2 | 3 | 4 | 5 | 從2換成1 |
| 🐐 | 🐐 | 🚗 | 🐐 | 🐐 | Lose |
| 🐐 | 🚗 | 🐐 | 🐐 | 🐐 | Lose |
| 🚗 | 🐐 | 🐐 | 🐐 | 🐐 | Win |
If \(A\) is a square matrix, then the minor of entry \(a_{ij}\) is denoted by \(M_{ij}\) and is defined to be the determinant of the submatrix that remains after the \(i\)th row and \(j\)th colomn are deleted from \(A\). The number \((-1)^{i+j}M_{ij}\) is denoted by \(C_{ij}\) and is called the cofactor of entry \(a_{ij}\).
If \(A\) is any \(n\times n\) matrix and \(C_{ij}\) is the cofactor of \(a_{ij}\), then the matrix \[ \begin{bmatrix} C_{11}&C_{12}&\cdots&C_{1n}\\ C_{21}&C_{22}&\cdots&C_{2n}\\ \vdots&\vdots&\ddots&\vdots\\ C_{n1}&C_{n2}&\cdots&C_{nn} \end{bmatrix} \] is called the matrix of cofactors from \(A\). The transpose of this matrix is called the adjoint of \(A\) and is denoted by by \(\text{adj}(A)\).
If \(A\) is an invertible matrix, then \[ A^{-1}=\frac{1}{\det{A}}\text{adj}(A) \]
零存整付的公式 \[ \begin{array}{rcl} \text{零存整付} &=&\text{每期固定存入的金額}\times [(1+\text{利率})^{\text{期數 }n}+(1+\text{利率})^{n-1}+\cdots+(1+\text{利率})] \\ &=& \text{每期固定存入的金額}\times \frac{(1+\text{利率})[(1+\text{利率})^{\text{期數}}-1]}{[(1+\text{利率})-1]} \end{array} \]
| one-to-one | not one-to-one | |
| onto | 1→4 2→5 3→6 | 1→4 2↗5 3↗ |
| not onto | 1→4 2→5 3→6 7 | 1→4 2↗5 3↗6 |
（未解決）若二次函數 \(ax^2+bx+c\) 通過四個象限，則 \(ac\lt 0\)。
數據更新標準差（這個不好用，直接用 \(x_1^2+x_2^2+\cdots=n_{\text{old}}(\mu_{\text{old}}^2+\sigma_{\text{old}}^2)\)，來推 \(x_1^2+x_2^2+\cdots=n_{\text{new}}(\mu_{\text{new}}^2+\sigma_{\text{new}}^2)\)）
| 舊數據 | 平移前 | 平移後 | 新數據 | 平移前 | 平移後 | |
| μ_old | ① | ④ | μ_new | ③ | ⑦ | |
| σ_old | ② | ⑤ | σ_new | X | ⑨ | |
| Σx²_old | X | ⑥ | Σx²_new | X | ⑧ |
進階性質
等差數列每n項和又成等差數列等比數列每n項和又成等比數列
\[ \begin{array}{rcllllllllllllllllll} S_n &=& a_1 &+& a_2 &+& a_3 &+& \cdots &+& a_n &=& a_1 &+& (a_1+d) &+& (a_1+2d) &+& \cdots &+& [a_1+(n-1)d] , \\ S_{n+1\sim 2n} &=& a_{n+1} &+& a_{n+2} &+& a_{n+3} &+& \cdots &+& a_{2n} &=& (a_1+nd) &+& [a_1+(n+1)d] &+& [a_1+(n+2)d] &+& \cdots &+& [a_1+(2n-1)d] , \\ S_{2n+1\sim 3n} &=& a_{2n+1} &+& a_{2n+2} &+& a_{2n+3} &+& \cdots &+& a_{3n} &=& (a_1+2nd) &+& [a_1+(2n+1)d] &+& [a_1+(2n+2)d] &+& \cdots &+& [a_1+(3n-1)d] \\ \end{array} \] \[ \begin{array}{rcl} S_n-S_{n+1\sim 2n} &=& nd\times n, \\ S_{2n+1\sim 3n}-S_{n+1\sim 2n} &=& nd\times n \end{array} \] \[ \begin{array}{rcllllllllllllllllll} S_n &=& a_1 &+& a_2 &+& a_3 &+& \cdots &+& a_n &=& a_1 &+& a_1 r &+& a_1 r^2 &+& \cdots &+& a_1 r^{n-1} , \\ S_{n+1\sim 2n} &=& a_{n+1} &+& a_{n+2} &+& a_{n+3} &+& \cdots &+& a_{2n} &=& a_1 r^n &+& a_1 r^{n+1} &+& a_1 r^{n+2} &+& \cdots &+& a_1 r^{2n-1} , \\ S_{2n+1\sim 3n} &=& a_{2n+1} &+& a_{2n+2} &+& a_{2n+3} &+& \cdots &+& a_{3n} &=& a_1 r^{2n} &+& a_1 r^{2n+1} &+& a_1 r^{2n+2} &+& \cdots &+& a_1 r^{3n-1} \\ \end{array} \] \[ \begin{array}{rcl} S_n÷S_{n+1\sim 2n} &=& r^n, \\ S_{2n+1\sim 3n}÷S_{n+1\sim 2n} &=& r^n \end{array} \]
The Irrational Conjugates Theorem Let \(f\) be a polynomial functiton with rational coefficients, and let \(a\) and \(b\) be rational numbers such that \(\sqrt{b}\) is irrational. If \(a+\sqrt{b}\) is a zero of \(f\), then \(a-\sqrt{b}\) is also a zero of \(f\).
Note that this theorem doesn't hold when the coefficients of \(f\) are not rational. For example, \((x-3)(x-\sqrt{3})\) only has an irrational root \(\sqrt{3}\).
The Complex Conjugates Theorem If \(f\) is a polynomial function with real coefficients, and \(a+bi\) is an imaginary zero of \(f\), then \(a-bi\) is also a zero of \(f\).
\(\sqrt{a}\sqrt{b}=\sqrt{ab}\) doesn't hold when \(a, b\) are not positive. For example, \(-1=i^2=\sqrt{-1}\sqrt{-1}\neq \sqrt{(-1)(-1)}=\sqrt{1}=1\).
| x³ | x=0 | -x³ | x=0 | x⁴ | x=0 | -x⁴ | x=0 | |||||||||||
| f | ↗ | ↗ | f | ↘ | ↘ | f | ↘ | ↗ | f | ↗ | ↘ | |||||||
| f' | + | 0 | + | f' | - | 0 | - | f' | - | 0 | + | f' | + | 0 | - | |||
| f'' | - | 0 | + | f'' | + | 0 | - | f'' | + | 0 | + | f'' | - | 0 | - | |||
| ∛x | x=0 | -∛x | x=0 | |∛x| | x=0 | -|∛x| | x=0 | |||||||||||
| f | ↗ | ↗ | f | ↘ | ↘ | f | ↘ | ↗ | f | ↗ | ↘ | |||||||
| f' | + | X | + | f' | - | X | - | f' | - | X | + | f' | + | X | - | |||
| f'' | + | X | - | f'' | - | X | + | f'' | - | X | - | f'' | + | X | + |
\[ -1 =(-1)^{\frac{1}{3}} =(-1)^{\frac{2}{6}} =\sqrt[6]{(-1)^2} =\sqrt[6]{1} =1 \] 小淳在清華求學時，每餐從台式炒飯、日式丼飯、義大利燉飯、韓國石鍋拌飯這4種餐點中擇一，且選擇餐點的習慣如下：
限制一：當天的午餐與前一天的午餐、晚餐不同。
限制二：當天的晚餐與前一天的午餐、晚餐不同。
假設 \(n\) 天內小淳選擇餐點的所有方法中，其中第 \(n\) 天的午、晚餐恰好吃相同餐點的方法數為 \(a_n\)，吃不同餐點的方法數為 \(b_n\)，\(T\) 為二階方陣且 \(\begin{bmatrix}a_n\\b_n\end{bmatrix}=T\begin{bmatrix}a_{n-1}\\b_{n-1}\end{bmatrix}\)，其中 \(n\) 為正整數且 \(n\geq 2\)。二階方陣 \(T\) 為何？Ans: \(\begin{bmatrix}3&2\\6&2\end{bmatrix}\)。
| 第一天 | 第二天 | |
| 午早相同 | \(a_1=4\) | \(a_2\) \(=\text{前一天午早相同方法數}\times 3\) \(+\text{前一天午早不同方法數}\times 2\) \(=3a_1+2b_1\) |
| 午早不同 | \(b_1=4\times 3=12\) | \(b_2\) \(=\text{前一天午早相同方法數}\times 3\times 2\) \(+\text{前一天午早不同方法數}\times 2\times 1\) \(=6a_1+2b_1\) |
系
| 直線系 | 圓系 | 平面系 |
| \(L_1:a_1x+b_1y+c_1=0\) \(L_2:a_2x+b_2y+c_2=0\) \(L_1\cap L_2=P\) 通過 \(P\) 的直線可設為 \((a_1x+b_1y+c_1)+k(a_2x+b_2y+c_2)=0\) | \(C_1:x^2+a_1x+y^2+b_1y+c_1=0\) \(C_2:x^2+a_2x+y^2+b_2y+c_2=0\) \(C_1\cap C_2=P, Q\) 通過 \(P, Q\) 的圓可設為 \((x^2+a_1x+y^2+b_1y+c_1)+k(x^2+a_2x+y^2+b_2y+c_2)=0\) | \(E_1:a_1x+b_1y+c_1z+d_1=0\) \(E_2:a_2x+b_2y+c_2z+d_2=0\) \(E_1\cap E_2=L\) 通過 \(L\) 的平面可設為 \((a_1x+b_1y+c_1z+d_1)+k(a_2x+b_2y+c_2z+d_2)=0\) |
北一女100教甄
兩正方形ABC與EFGH邊長均為1，其中ABCD固定平放在直線L上，如右圖所示。若正方形EFGH之一頂點H在CD上移動，且另一頂點G在直線L上移動，當BE=BF時，CG= Ans:(-1+√3)/2
令F在L上的垂足為K。過E做L的平行線M，延長AB、CD、FK分別交M於P、Q、R。
令∠HGC=θ，則CG=cos θ，GK=sin θ，FK=cos θ，RF=sin θ，QE=sin θ，PQ=1。且PB=sin θ+cos θ。
\[ \overline{BE}^2 =\overline{PB}^2+\overline{PE}^2 =(\sin{\theta}+\cos{\theta})^2+(1+\sin{\theta})^2 \]
\[ \overline{BF}^2 =\overline{BK}^2+\overline{FK}^2 =(1+\cos{\theta}+\sin{\theta})^2+\cos^2{\theta} \]
兩者相等解方程式。
摸彩原理：若干人依序排隊摸彩，取後不放回，在摸彩活動尚未進行之前，可計算得知每個人中獎的機率都一樣大，無論誰先誰後。
籤筒有3支中獎和8支銘謝惠顧的籤。甲、乙、丙3人依序抽籤，取後不放回，求
(1)甲中籤的機率為\(\frac{3}{11}\)
(2)乙中籤的機率為\(\frac{3}{11}\)
(3)丙中籤的機率為\(\frac{3}{11}\)
甲中獎的機率可以轉化成 \(w_1\) 或 \(w_2\) 或 \(w_3\) 排第一個的機率，也就是 \(\frac{C^3_1\times 10!}{11!}\)。
乙中獎的機率可以轉化成 \(w_1\) 或 \(w_2\) 或 \(w_3\) 排第二個的機率，也就是 \(\frac{C^3_1\times 10!}{11!}\)。
丙中獎的機率可以轉化成 \(w_1\) 或 \(w_2\) 或 \(w_3\) 排第三個的機率，也就是 \(\frac{C^3_1\times 10!}{11!}\)。
一般來說，籤筒有 \(m\) 支中獎和 \(n\) 支銘謝惠顧的籤。依序抽籤，取後不放回，求第 \(k\) 個人中籤的機率為 \(\frac{m}{m+n}\)。
來看另一題
袋中有2個黃球、3個綠球及4個紅球，逐一取出且不放回，求：
(1) 紅球最後被取完的機率為 \(\frac{4}{9}\)
(1) 紅球最後被取完的機率為 \(\frac{2}{3}\)
(1) 這題可以用排列組合的方法來思考，假設黃球編號為 \(y_1, y_2\)，綠球編號為 \(g_1, g_2, g_3\)，紅球編號為 \(r_1, r_2, r_3, r_4\)，則每一種取球結果就是這幾顆編號球的排列，所以紅球最後被取完就是 \(r_1\) 或 \(r_2\) 或 \(r_3\) 排最後一位的排法，共有 \(C^4_1\times 8!\) 種，所以紅球最後被取完的機率就是 \(\frac{C^4_1\times 8!}{9!}=\frac{4}{9}\)。
(2) 這題可以忽略綠球，我們來說明為什麼。
假設題目只有2個黃球、4個紅球，則黃球比紅球先被取完的機率就是紅球排最後一個的機率，也就是 \(\frac{C^4_1\times 5!}{6!}=\frac{4}{6}=\frac{2}{3}\)。
現在考慮有綠球的情況，一樣把這幾顆編號色球排列，我們先選出3個位置來放綠球，就是 \(P^9_3\) 種選法。剩下的位置放黃球跟紅球，這些黃球跟紅球要滿足黃球比紅球先被取完，也就是紅色球要擺在最後一個，這剛剛已經算過了，總共有 \(C^4_1\times 5!\) 種排法，所以機率是 \(\frac{C^4_1\times 5!\times P^9_3}{9!}=\frac{C^4_1\times 5!}{6!}=\frac{4}{6}=\frac{2}{3}\)。
我們可以推出一般情形下的公式。假設有 \(y\) 個黃球、\(g\) 個綠球、\(r\) 個紅球，則黃球比紅球先被取完的機率為 \[ \frac{(y+r-1)!\times C^r_1\times P^{y+g+r}_{g}}{(y+g+r)!} = \frac{(y+r-1)!\times C^r_1}{(y+r)!} \] 化簡之後等式右邊的機率相當於沒有綠球的情況下，黃球比紅球先被取完的機率。
下面是另一種思路。
袋中有3白球、4紅球、5黑球，依序取出，取後不放回，則紅球先取完的機率為
| ↗5/9 | 2色中，黑最後 | ||
| 3色中，白最後 | |||
| ↗3/12 | ↘4/9 | 2色中，紅最後 | |
| ↘5/12 | ↗3/7 | 2色中，白最後 | |
| 3色中，黑最後 | |||
| ↘4/7 | 2色中，紅最後 |
下面題目皆可以用，「射未知，代入已知」來解，皆選自對話式數學4A。
| \(A\) | ||
| → | ||
| 已知方程式 | 未知 \(\begin{bmatrix}x\\y\end{bmatrix}\) | |
| ← | ||
| \(A^{-1}\) |
●p.236, exa.5.1 \(A=\begin{bmatrix}3&2\\1&4\end{bmatrix}\)，直線 \(2x+3y=6\) 經 \(A\) 變換後的圖形方程式為。Ans: x+y=12
| \(A=\begin{bmatrix}3&2\\1&4\end{bmatrix}\) | ||
| → | ||
| 已知 \(2x+3y=6\) | 未知 \(\begin{bmatrix}x\\y\end{bmatrix}\) | |
| ← | ||
| \(A^{-1}=\frac{1}{10}\begin{bmatrix}4&-2\\-1&3\end{bmatrix}\) |
代入已知：\(2\cdot \frac{4x-2y}{10}+3\cdot \frac{-x+3y}{10}=6\)。
●p.237, exa.5.2 已知方陣 \(A=\begin{bmatrix}1&4\\2&3\end{bmatrix}\)，經 \(A\) 變換後的圖形為 \(3x-2y=1\)，試求出線性變換前的圖形方程式為。Ans: x-6y=-1
| \(A=\begin{bmatrix}1&4\\2&3\end{bmatrix}\) | ||
| → | ||
| 未知 \(\begin{bmatrix}x\\y\end{bmatrix}\) | 已知 \(3x-2y=1\) | |
代入已知：\(3(x+4y)-2(2x+3y)=1\)。
●p.239, exa.7.1 \(A=\begin{bmatrix}2&1\\0&3\end{bmatrix}\)，求圓 \(x^2+y^2=1\) 經 \(A\) 變換後的圖形方程式為。Ans: \(9x^2-6xy+5y^2=36\)
●p.239, exa.7.2 \(A=\begin{bmatrix}2&0\\-1&3\end{bmatrix}\)，曲線 \(\Gamma\) 經 \(A\) 變換後的圖形為 \(\Gamma':y=x^2+3x+1\)，求 \(\Gamma\) 的方程式為。Ans: \(4x^2+7x-3y+1=0\)
●p.241, exa.8.2 平面上直線 \(3x+5y=10\) 繞原點逆時針旋轉 \(45^{\circ}\) 後的方程式為。Ans: \(-x+4y=5\sqrt{2}\)
●p.241, exa.8.3 試求平面上圓 \(x^2+y^2+4x-8y-1=0\) 經 \(\begin{bmatrix}\cos{30^{\circ}}&-\sin{30^{\circ}}\\\sin{30^{\circ}}&\cos{30^{\circ}}\end{bmatrix}\) 變換後所得圖形方程式為。Ans: \((x+\sqrt{3}+2)^2+(y+1-2\sqrt{3})^2=21\)
●p.246, exa.10.1 點 \((x, y)\) 對 \(x\) 軸鏡射，其平面變換為 \((x, y)\to (x, -y)\)，寫成二階方陣為 \(\begin{bmatrix}1&0\\0&-1\end{bmatrix}\)，直線 \(3x+2y=7\) 經過此平面變換所成新圖形的方程式為 Ans: 3x-2y=7
●p.246, exa.10.2 將點 \((x, y)\) 對直線 \(x-y=0\) 鏡射，其平面變換為 \((x, y)\to (y, x)\)，寫成二階方陣為 \(\begin{bmatrix}0&1\\1&0\end{bmatrix}\)，直線 \(5x-7y=1\) 經過此平面變換所成新圖形的方程式為 Ans: 5y-7x=1
●p.248, exa.11.1 若 \(y=5x^2\) 在 \((x, y)\to (3x, 2y)\) 的伸縮變換下變成另一圖形，求此新圖形的方程式為 Ans: 9y=10x
●p.248, exa.11.2 平面上有一個圓 \(C:(x+3)^2+(y-2)^2=25\)，經過伸縮矩陣 \(\begin{bmatrix}4&0\\0&3\end{bmatrix}\) 變換後的圖形為 \(\Gamma\)，其方程式為 \(\left(\frac{x}{4}+3\right)^2+\left(\frac{y}{3}-2\right)^2=25\)，圖形 \(\Gamma\) 的面積為 \(300\pi\) 平方單位。
●p.249, exa.12.1 若直線 \(L:3x-4y=5\) 在 \((x, y)\to (x+2y, y)\) 的推移下變換成另一直線 \(L'\)，求 \(L'\) 的方程式為 \(3(x-2y)-4y=5\)
●p.249, exa.12.2 坐標平面上直線 \(L:x=3\)，經推移變換 \(\begin{bmatrix}1&k\\0&1\end{bmatrix}\) 作用後變成 \(L'\)，且 \(L'\) 經過點 \((15, 2)\)，求 \(k=6\)。
x為正實數，\(x^2-3x-1=0\)，求 \(x^3+x^2+x^{-2}-x^{-3}\)? Ans: 47 解：由 \(x^2-1=3x\)，同除以 \(x\) 得 \(x-\frac{1}{x}=3\)，後面用平方和、立方差公式。
從0，1，2，3，4，5之中任取4個不同的數字排成四位數，則所有排成的四位數總和為何？
千位數是1的數字有5*4*3=60個，這些數字的千位數加起來是1000*60 千位數是2的數字有5*4*3=60個，這些數字的千位數加起來是2000*60 千位數是3的數字有5*4*3=60個，這些數字的千位數加起來是3000*60 千位數是4的數字有5*4*3=60個，這些數字的千位數加起來是4000*60 千位數是5的數字有5*4*3=60個，這些數字的千位數加起來是5000*60 以上，總和是900000 百位數是1的數字有4*4*3=48個，這些數字的百位數加起來是100*48 百位數是2的數字有4*4*3=48個，這些數字的百位數加起來是200*48 百位數是3的數字有4*4*3=48個，這些數字的百位數加起來是300*48 百位數是4的數字有4*4*3=48個，這些數字的百位數加起來是400*48 百位數是5的數字有4*4*3=48個，這些數字的百位數加起來是500*48 以上，總和是72000 十位數是1的數字有4*4*3=48個，這些數字的十位數加起來是10*48 十位數是2的數字有4*4*3=48個，這些數字的十位數加起來是20*48 十位數是3的數字有4*4*3=48個，這些數字的十位數加起來是30*48 十位數是4的數字有4*4*3=48個，這些數字的十位數加起來是40*48 十位數是5的數字有4*4*3=48個，這些數字的十位數加起來是50*48 以上，總和是7200 個位數是1的數字有4*4*3=48個，這些數字的個位數加起來是1*48 個位數是2的數字有4*4*3=48個，這些數字的個位數加起來是2*48 個位數是3的數字有4*4*3=48個，這些數字的個位數加起來是3*48 個位數是4的數字有4*4*3=48個，這些數字的個位數加起來是4*48 個位數是5的數字有4*4*3=48個，這些數字的個位數加起來是5*48 以上，總和是720 加起來是979920
| 兩點式 | \(\frac{y-y_1}{x-x_1}=\frac{y_1-y_2}{x_1-x_2}, y-y_1=\frac{y_1-y_2}{x_1-x_2}(x-x_1)\) |
| 點斜式 | \(y-y_1=m(x-x_1)\) |
| 斜截式 | \(y=mx+b\)（用點斜式推） |
| 截距式 | \(\frac{x}{a}+\frac{y}{b}=1\)（用兩點式推） |
| 一般式 | \(ax+by+c=0\) |
數學雜題
✍️🙋♂️🙋♀️🧑🏫👨🏫👩🏫📖📅空間中有一 \(\triangle ABC\)，其中 \(A(8, -11, -2)\)，若 \(\angle B\) 與 \(\angle C\) 的內角平分線分別為 \(L_1:\frac{x}{1}=\frac{y}{2}=\frac{z}{2}, L_2:\frac{x-3}{2}=\frac{y}{1}=\frac{z-2}{2}\)，則直線 \(BC\) 的比例式為？
求 \(A\) 在 \(L_1\) 上的投影點 \((-2, -4, -4)\)，
求 \(A\) 對 \(L_1\) 的對稱點 \(P(-12, 3, -6)\)。
則 \(P\) 會在 \(\overleftrightarrow{BC}\) 上。
求 \(A\) 在 \(L_2\) 上的投影點 \((1, -1, 0)\)，
求 \(A\) 對 \(L_2\) 的對稱點 \(Q(-6, 9, 2)\)。
則 \(Q\) 會在 \(\overleftrightarrow{BC}\) 上。
\(BC\) 的比例式為 \(\frac{x+6}{6}=\frac{y-9}{6}=\frac{z-2}{8}\)。
在△ABC中，已知A(4, -5)，若∠B、∠C之角平分線分別為L₁:x+y=3，L₂:x-3y=-11，試求直線BC的斜率為Ans:-7/5（學測模公私立高中112第三次）
三角形ABC中,A(2,-4),若∠B,∠C之角平分線分別為L1:x+y-2=0及L2:x-3y-6=0,則BC直線之方程式為?
x+7y-6=0
空間中三個點 \(A(0, 1, 2), B(-1, 0, 3), C(1, 2, 3)\)，則三角形 \(\triangle ABC\) 的外心坐標為？
求 \(\overline{AB}\) 的中垂面為 \(2x+2y-2z=-5\)，
求 \(\overline{AC}\) 的中垂面為 \(2x+2y+2z=9\)，
求 \(\overline{BC}\) 的中垂面為 \(x+y-1=0\)，
接著求 \(A, B, C\) 所在的平面為 \(x-y+1=0\)，
求上面幾個平面的交點得 \((0, 1, \frac{7}{2})\)。
（哲毅高二下二段難題，未解決）空間中平面 \(E:-x+y+2z-10=0\)，直線 \(L:\frac{x-2}{1}=\frac{y+2}{-1}=\frac{z-1}{3}\)，直線 \(L\) 與平面 \(E\) 的交點為 \(A\)，若自直線 \(L\) 上之點 \(P\) 向平面 \(E\) 做垂線，垂足為 \(Q\)，使三角形 \(\triangle APQ\) 面積為 \(\frac{20\sqrt{2}}{3}\)，求 \(P\) 的坐標。
Cube Cross Sections
龍騰數學4A 進階卷 第8回單元7條件機率與貝氏定理 四、1 已知有寫著1、2、3、4、5的球各2顆，將其中隨機5顆放入A箱，其餘5顆放入B箱。箱子內所有球的數字乘積的個位數為箱子點數，則 (1)兩個箱子點數皆為0的機率為和？ (2)已知A箱點數為0，則兩個箱子點數皆為0的條件機率為何？ (1) 全部 減A55XXX 減B55XXX 減A(大5)1133 減A(小5)1133 減B(大5)1133 減B(小5)1133\[ \frac{C^{10}_{5}-C^8_3-C^8_3-C^2_1\times C^2_1}{C^{10}_5} \] (2)
全部 減A55奇奇奇 減B55XXX 減A(大5)1133 減A(小5)1133\[ \frac{\frac{C^{10}_{5}-C^4_3-C^8_3-C^2_1\times C^1_1}{C^{10}_5}}{\frac{C^{10}_{5}-C^8_3-C^8_3-C^2_1\times C^2_1}{C^{10}_5}} \]
翰林數學2 A卷 第8回3-2排列 四、1 從0，1，2，3，4，5之中任取4個不同的數字排成四位數，則： 3. 所有排成的四位數總和為和？ 千位數是1個數字有5*4*3=60個，這些數字的千位數加起來是1000*60 千位數是1個數字有5*4*3=60個，這些數字的千位數加起來是2000*60 千位數是1個數字有5*4*3=60個，這些數字的千位數加起來是3000*60 千位數是1個數字有5*4*3=60個，這些數字的千位數加起來是4000*60 千位數是1個數字有5*4*3=60個，這些數字的千位數加起來是5000*60 以上，總和是900000 百位數是1的數字有4*4*3=48個，這些數字的百位數加起來是100*48 百位數是2的數字有4*4*3=48個，這些數字的百位數加起來是200*48 百位數是3的數字有4*4*3=48個，這些數字的百位數加起來是300*48 百位數是4的數字有4*4*3=48個，這些數字的百位數加起來是400*48 百位數是5的數字有4*4*3=48個，這些數字的百位數加起來是500*48 以上，總和是72000 十位數是1的數字有4*4*3=48個，這些數字的十位數加起來是10*48 十位數是2的數字有4*4*3=48個，這些數字的十位數加起來是20*48 十位數是3的數字有4*4*3=48個，這些數字的十位數加起來是30*48 十位數是4的數字有4*4*3=48個，這些數字的十位數加起來是40*48 十位數是5的數字有4*4*3=48個，這些數字的十位數加起來是50*48 以上，總和是7200 加起來是979920
對話式p.112, exa.8.3 正10邊形共有35條對角線，其10個頂點可決定40個直角三角形，60個頓角三角形。 考慮正十邊形的外接圓， 一個邊對應的圓心角是360°/10=36°， 一個邊對應的圓周角是36°/2=18° 選定一個點當作鈍角，這個鈍角必須包含至少6個相鄰邊對應的圓周角 （因為18°*5=90°，18°*6=108°>90°） 所以有下列1+2+3=6種可能。 這1個鈍角包含八個相鄰圓周角 這2個鈍角包含七個相鄰圓周角 這3個鈍角包含六個相鄰圓周角 所以每一個頂點當鈍角都可以決定6個鈍角三角形，而共有10個頂點，所以共有6*10=60個鈍角三角形。
國一下不等式，確定當選最少票數問題
題目：有 \(n\) 位候選人，要選出 \(m\) 位，共有 \(p\) 票，請問得幾票就確定當選？
解法：假設 \(n\) 位候選人的得票數由大到小排列為 \[x_1 \geq x_2 \geq \cdots \geq x_m \color{red}{>} x_{m+1} \geq \cdots \geq x_{n} \geq 0.\] 於是我們有 \[ \begin{array}{lcl} p &=&\underline{x_1+x_2+\cdots+x_m+x_{m+1}}+x_{m+2} \cdots +x_{n} \\ &\stackrel{x_1 \geq x_2 \geq \cdots \geq x_m \geq x_{m+1}}{\geq}& \underbrace{x_{m+1}+x_{m+1}+\cdots +x_{m+1}+x_{m+1}}_{m+1 \text{ times}}+x_{m+2}+ \cdots +x_{n} \\ &\geq& \underline{(m+1)\cdot x_{m+1}}+x_{m+2}+ \cdots +x_{n} \\ &\stackrel{\color{red}{x_{m+2}} \geq \cdots \geq x_{n} \geq 0}{\geq}& (m+1)\cdot x_{m+1}. \end{array} \] 所以 \[\frac{p}{m+1} \geq x_{m+1}.\] 只要得 \(\left\lfloor \frac{p}{m+1}\right\rfloor+1\) 票（或以上）即確定當選。其中 \(\lfloor x\rfloor\) 是地板符號，也就是取不超過 \(x\) 的最大整數。
（未解決）已知非零實數 \(a\gt b\gt c\)，方程組 \(\left\{\begin{array}{l}a=b(1-c)\\b=c(1-a)\\c=a(1-b)\end{array}\right.\) 恰有一組解，試選出正確的選項。
(1) \((1-a)(1-b)(1-c)=1\)
(2) \(ab+bc+ca=0\)
(3) \(a^2+b^2+c^2=3abc\)
(4) \(abc\lt 0\)
(5) \(a+b+c\lt 0\)
Ans:1, 2, 4
相乘得(1)，相加得(2)。將(1)展開可得 \(abc=-(a+b+c)\)。
龍騰數學4A 進階卷 第6回單元5空間中的平面 一、2 空間中6個平面Γ₁：2x+y+z=0、Γ₂：2x+y+z=8、Γ₃：x+2y+z=0、Γ₄：x+2y+z=8、Γ₅：x+y+2z=0、Γ₆：x+y+2z=8所圍成的平行六面體體積為下列哪一個選項？ Ans: 128 \[ \begin{array}{lll} \Gamma_1\cap \Gamma_3\cap \Gamma_6=\{(x_1, y_1, z_1)\}, & \text{substitute }(x_1, y_1, z_1)\text{ into }\Gamma_1, \Gamma_3, \Gamma_6, & \left\{\begin{array}{lll}2x_1+y_1+z_1=0\\x_1+2y_1+z_1=0\\x_1+y_1+2z_1=8\end{array}\right., \\ \Gamma_1\cap \Gamma_4\cap \Gamma_5=\{(x_2, y_2, z_2)\}, & \text{substitute }(x_2, y_2, z_2)\text{ into }\Gamma_1, \Gamma_4, \Gamma_5, & \left\{\begin{array}{lll}2x_2+y_2+z_2=0\\x_2+2y_2+z_2=8\\x_2+y_2+2z_2=0\end{array}\right., \\ \Gamma_2\cap \Gamma_3\cap \Gamma_5=\{(x_3, y_3, z_3)\}, & \text{substitute }(x_3, y_3, z_3)\text{ into }\Gamma_2, \Gamma_3, \Gamma_5, & \left\{\begin{array}{lll}2x_3+y_3+z_3=8\\x_3+2y_3+z_3=0\\x_3+y_3+2z_3=0\end{array}\right.. \end{array} \] Transform these equations into a matrix form \[ \begin{bmatrix}2&1&1\\1&2&1\\1&1&2\end{bmatrix} \begin{bmatrix}x_1&x_2&x_3\\y_1&y_2&y_3\\z_1&z_2&z_3\end{bmatrix} = \begin{bmatrix}0&0&8\\0&8&0\\8&0&0\end{bmatrix} \] Apply determinant on both sides.
如圖。空間中，平面 \(ABCD\) 為 \(\Gamma_1:x=y+z\)、平面 \(EFGH\) 為 \(\Gamma_2\)、平面 \(ADHE\) 為 \(\Lambda_1:y=x+z\)、平面 \(BCGF\) 為 \(\Lambda_2\)、平面 \(ABFE\) 為 \(\Omega_1:z=x+y\)、平面 \(CDHG\) 為 \(\Omega_2\)。上下兩平面 \(\Gamma_2\)、\(\Gamma_1\) 互相平行且距離為 \(2\)，左右兩平面 \(\Lambda_2\)、\(\Lambda_1\) 互相平行且距離為 \(4\)，前後兩平面 \(\Omega_1\)、\(\Omega_2\) 互相平行且距離為 \(6\)。而且，正四面體中，稜長與高的比為 \(\sqrt{6}:2\)，利用以上資訊，可以推得此六個平面所圍成的平行六面體體積為下列哪一個選項？ Ans: \(36\sqrt{3}\)
空間中有一個平面 \(x-y+2z+1=0\)。從 \((1, 2, -3)\) 發射一道光，射向此平面上的一點 \((-1, 0, 0)\)，試問反射後的光會通過下列哪些點？ (1) \((-5, 0, -1)\) (2) \((1, 0, \frac{1}{2})\) (3) \((-3, 0, -\frac{1}{2})\) (4) \((-13, 0, -3)\) Ans:(3)(4) （南一學測4568）
99指考數甲 選填D
一個抽獎活動依排隊順序抽獎，輪到抽獎的人有一次抽獎機會，抽獎方式為丟擲一枚公正銅板，正面為中獎，反面為沒中獎。獎品有三份，活動直到三份獎品都被抽中為止。則在排第四位的人可以抽獎的情況下，排第五位的人可以抽獎的條件機率為 Ans: 11/14
第五位可抽∩第四位可抽=第五位可抽
從反面算，第五位不可抽的情形只有OOO，OOXO，OXOO，XOOO，機率是 \(\frac{1}{8}+\frac{1}{16}+\frac{1}{16}+\frac{1}{16}=\frac{5}{16}\)
從反面算，第四位不可抽的情形只有OOO，機率是1/8
\[ \begin{array}{rcl} 所求&=& P(第五位可抽|第四位可抽) \\ &=& \frac{P(第五位可抽∩第四位可抽)}{P(第四位可抽)} \\ &=& \frac{P(第五位可抽)}{P(第四位可抽)} \\ &=& \frac{[1-P(第五位不可抽)]}{[1-P(第四位不可抽)]} \end{array} \] 影片解析
這個題目的樣本空間是無限大
| OOO | \(\frac{1}{2^3}\) |
| XOOO OXOO OOXO |
\(\frac{3}{2^4}\) |
| XXOOO XOXOO XOOXO OXXOO OXOXO OOXXO |
\(\frac{6}{2^5}\) |
| ... |
總和為 \(\sum_{n=1}^{\infty}\frac{\frac{n(n+1)}{2}}{2^{n+2}}=1\)
平面上n條直線，最多可以將平面分成aₙ個區域，\(a_n=\frac{n^2+n+2}{2}\)
空間中n個平面，最多可以將空間分成bₙ個區域，\(b_n=\frac{n^3+5n+6}{6}\)
aₙ稱為Lazy caterer's sequence，bₙ稱為cake number。
bₙ公式的證明簡述如下：假設空間中已經有n個平面，將空間分割成最多bₙ個區塊，現在加入第n+1個平面E。平面E會與前n個平面相交於n條直線，這n條直線會把平面E分割成 \(aₙ=\frac{n^2+n+2}{2}\) 個區域，這 \(\frac{n^2+n+2}{2}\) 個區域，又分別可以將其所在的區塊，再分別切出多一個區塊，所以可以將空間分割成最多 \(b_{n+1}=bₙ+\frac{n^2+n+2}{2}\)，個區塊。解這個遞迴就可以得到 \(bₙ=\frac{n^3+5n+6}{6}\)。讀者自己想想n=2的情形。
兩個公式的證明參考Challenging Mathematical Problems with Elementary Solutions。這本書有100題，上述的問題在p.13, problem 44.a及45.a，證明在p.102。problem 45.a的證明要用到44.a的結果。
$$ \begin{array}{lll} \displaystyle x&=& \displaystyle \frac{\begin{bmatrix}-3c_1&2a_1-b_1\\-3c_2&2a_2-b_2\end{bmatrix}}{\begin{bmatrix}a_1&2a_1-b_1\\a_2&2a_2-b_2\end{bmatrix}} \\ &=& \displaystyle \frac{\begin{bmatrix}-3c_1&2a_1-b_1\\-3c_2&2a_2-b_2\end{bmatrix}}{\begin{bmatrix}a_1&-b_1\\a_2&-b_2\end{bmatrix}} \\ &=& \displaystyle \frac{(-3)\cdot 2\cdot \begin{bmatrix}c_1&a_1\\c_2&a_2\end{bmatrix}+(-3)\cdot (-1)\cdot \begin{bmatrix}c_1&b_1\\c_2&b_2\end{bmatrix}}{(-1)\cdot \begin{bmatrix}a_1&b_1\\a_2&b_2\end{bmatrix}} \\ &=& \displaystyle -6\cdot \frac{\begin{bmatrix}a_1&c_1\\a_2&c_2\end{bmatrix}}{\begin{bmatrix}a_1&b_1\\a_2&b_2\end{bmatrix}}-3\cdot \frac{\begin{bmatrix}c_1&b_1\\c_2&b_2\end{bmatrix}}{\begin{bmatrix}a_1&b_1\\a_2&b_2\end{bmatrix}}\\ &=& \displaystyle -6\cdot 2-3\cdot 1\\ &=& \displaystyle -15. \end{array} $$
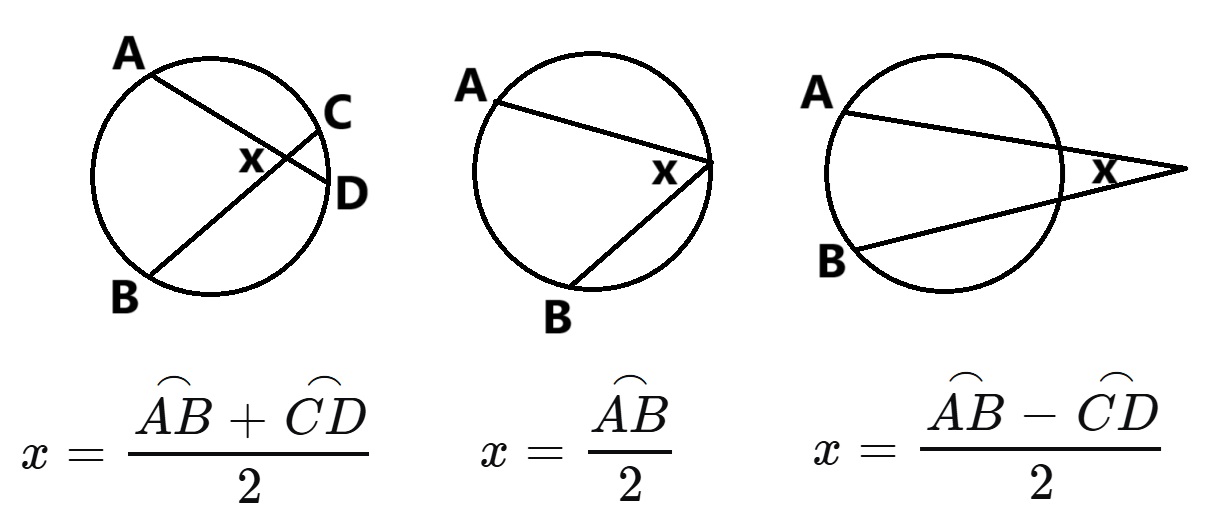
圓內角，圓周角，圓外角，注意到圓周角是圓內角或是圓外角的特例
有兩等差數列，其前n項和之比為(3n+1):(7n-11)，則此二數列第6項的比為？
Ans: 17:33
\[
\begin{array}{ccccc}
a_1+a_{11} &=& 2a_1+10d &=& 2a_6, \\
a_2+a_{10} &=& 2a_1+10d &=& 2a_6,
\end{array}
\]
6.6+66.66+666.666+...+至第n項
\[
\begin{array}{ll}
& 6.6+66.66+666.666+\cdots+\underbrace{6\cdots 6}_{n\text{ times}}.\underbrace{6\cdots 6}_{n\text{ times}} \\
=& 6(1.1+11.11+111.111+\cdots+\underbrace{1\cdots 1}_{n\text{ times}}.\underbrace{1\cdots 1}_{n\text{ times}}) \\
=& \frac{6}{9}(9.9+99.99+999.999+\cdots+\underbrace{9\cdots 9}_{n\text{ times}}.\underbrace{9\cdots 9}_{n\text{ times}}) \\
=& \frac{6}{9}\left[\left(10-0.1\right)+\left(100-0.01\right)+\cdots +\left(1\underbrace{0\cdots 0}_{n\text{ times}}-0.\underbrace{0\cdots 0}_{n-1\text{ times}}1\right)\right] \\
=& \frac{6}{9}\left[\left(10-\frac{1}{10}\right)+\left(100-\frac{1}{100}\right)+\cdots +\left(1\underbrace{0\cdots 0}_{n\text{ times}}-\frac{1}{1\underbrace{0\cdots 0}_{n\text{ times}}}\right)\right] \\
=& \frac{6}{9}\left[\left(10-\frac{1}{10}\right)+\left(10^2-\frac{1}{10^2}\right)+\cdots +\left(10^n-\frac{1}{10^n}\right)\right] \\
\end{array}
\]
設a、b為整數，且 \(\frac{5}{a}-\frac{4}{b}=3\)，則數對(a, b)共有幾組解？Ans: 5 \[ \begin{array}{lll} \frac{5}{a}-\frac{4}{b}=3 & \Rightarrow & 5b-4a=3ab \\ & \Rightarrow & 3ab+4a-5b=0 \\ & \Rightarrow & (3a-5)(b+\frac{4}{3})=\frac{-20}{3} \\ & \Rightarrow & (3a-5)(3b+4)=-20 \end{array} \] 窮舉討論。
直角三角形整數邊長
3:4:5
6:8:10
5:12:13
15:20:25
7:24:25
8:15:17
20:21:29
高中數學第一冊第一章：絕（絕對值）、乘（乘法公式）、根（根式）、算（算幾不等式）、指對（指數與對數）
華盛頓高中數學自編教材目錄 高一上v1 第一章 數與式 1-1 數與數線 1-2 式的運算 第二章 指數與對數 2-1 指數 2-2 常用對數 第三章 多項式函數 3-1 多項式的運算與應用 3-2 簡單多項式函數及其圖形 3-3 多項式函數的圖形與多項式不等式 第四章 直線與圓 4-1 直線方程式及其圖形 4-2 直線方程式的應用 4-3 圓與直線的關係 高一下v2 第一章 數列與級數 1-1 數列與級數 1-2 數學歸納法與遞迴關係式 第二章 排列與組合 2-1 邏輯、集合與計數原理 2-2 排列 2-3 組合 2-4 機率 第三章 數據分析 3-1 一維數據分析 3-2 二維數據分析 第四章 三角比 4-1 直角三角形的三角比 4-2 廣義角的三角比 4-3 三角比性質 高二上v3 第一章 （未完成） 第二章 指數與對數函數 2-1 指數函數及其圖形 2-2 對數與對數律 2-3 對數函數及其圖形 2-4 指數與對數函數的應用 第三章 平面向量 3-1 平面向量的表示法 3-2 平面向量的內積 3-3 面積與二階行列式 高三下v4 第一章 向量空間 1-1 空間概念 1-2 空間向量的坐標表示法 1-3 空間向量的內積 1-4 外積、體積與行列式 第二章 空間中的平面與直線 2-1 平面方程式 2-2 空間直線方程式 第三章 機率 3-1 主觀機率與客觀機率 3-2 條件機率與獨立事件 3-3 貝氏定理 第四章 矩陣 4-1 高斯消去法與矩陣 4-2 矩陣的運算 4-3 矩陣的應用 華盛頓高中分班 精英班 普通班（英語資優班） 寰宇班（雙語實驗班） 國語資優班 數理資優班
指數與對數
| 底同指不同 | ||
| \(a^m a^n=a^{m+n}\) | ||
| \(\frac{a^m}{a^n}=a^{m-n}\) | ||
| 指同底不同 | ||
| \((ab)^n=a^n b^n\) | \(\sqrt[n]{ab}=\sqrt[n]{a}\sqrt[n]{b}\) | \((ab)^{\frac{1}{n}}=a^{\frac{1}{n}}b^{\frac{1}{n}}\) |
| \(\left(\frac{a}{b}\right)^n=\frac{a^n}{b^n}\) | \(\sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}}\) | \(\left(\frac{a}{b}\right)^{\frac{1}{n}}=\frac{a^{\frac{1}{n}}}{b^{\frac{1}{n}}}\) |
| 指數相乘 | ||
| \((a^m)^n=a^{mn}\) |
| Exponential | translation | Logarithmic |
| \(x=a^m\) | → | \(\log_a{x}=m\) |
| \(y=a^n\) | → | \(\log_a{y}=n\) |
| \(xy=a^m\cdot a^n=a^{m+n}\) | → | \(\log_a{xy}=m+n\)\(=\log_a{x}+\log_a{y}\) |
三角函數
沒什麼規律，不好記
| 270°－θ | 180°－θ | 90°－θ | －θ | 90°＋θ | 180°＋θ | 270°＋θ | |
| sin | －cos θ | ＋sin θ | ＋cos θ | －sin θ | ＋cos θ | －sin θ | －cos θ |
| cos | －sin θ | －cos θ | ＋sin θ | ＋cos θ | －sin θ | －cos θ | ＋sin θ |
| tan | \(\frac{1}{\tan{\theta}}\) | －tan θ | \(\frac{1}{\tan{\theta}}\) | －tan θ | \(\frac{－1}{\tan{\theta}}\) | ＋tan θ | \(\frac{－1}{\tan{\theta}}\) |
| ▢－270° | ▢－180° | ▢－90° | ▢ | ▢＋90° | ▢＋180° | ▢＋270° | |
| sin | ＋cos▢ | －sin▢ | －cos▢ | ＋sin▢ | ＋cos▢ | －sin▢ | －cos▢ |
| cos | －sin▢ | －cos▢ | ＋sin▢ | ＋cos▢ | －sin▢ | －cos▢ | ＋sin▢ |
| tan | －1/tan▢ | ＋tan▢ | －1/tan▢ | ＋tan▢ | －1/tan▢ | ＋tan▢ | －1/tan▢ |
| －▢－270° | －▢－180° | －▢－90° | －▢ | －▢＋90° | －▢＋180° | －▢＋270° | |
| sin | ＋cos▢ | ＋sin▢ | －cos▢ | －sin▢ | ＋cos▢ | ＋sin▢ | －cos▢ |
| cos | ＋sin▢ | －cos▢ | －sin▢ | ＋cos▢ | ＋sin▢ | －cos▢ | －sin▢ |
| tan | ＋1/tan▢ | －tan▢ | ＋1/tan▢ | －tan▢ | ＋1/tan▢ | －tan▢ | 1/tan▢ |
Sums of Sines and Cosines
If \(A\) and \(B\) are real numbers, then \[ A\sin{x}+B\cos{x}=k\sin{(x+\phi)} \] where \(k=\sqrt{A^2+B^2}\) and \(\phi\) satisfies \[ \cos{\phi}=\frac{A}{\sqrt{A^2+B^2}} \text{ and } \sin{\phi}=\frac{B}{\sqrt{A^2+B^2}} \]
令 \(f(x)=A\sin{x}+B\cos{x}=k\sin{(x+\phi)}\)，
當 \(\sin{x}=\frac{A}{\sqrt{A^2+B^2}}\) 及 \(\cos{x}=\frac{B}{\sqrt{A^2+B^2}}\) 時，\(f(x)\) 有最大值 \(\sqrt{A^2+B^2}\)。
當 \(\sin{x}=\frac{-A}{\sqrt{A^2+B^2}}\) 及 \(\cos{x}=\frac{-B}{\sqrt{A^2+B^2}}\) 時，\(f(x)\) 有最小值 \(-\sqrt{A^2+B^2}\)。
證明：當 \(x+\phi=90^{\circ}\) 時，\(\sin{(x+\phi)}=1\) 且 \(f(x)\) 有最大值 \(\sqrt{A^2+B^2}\)。
而當 \(x+\phi=90^{\circ}\) 時，\(x=90^{\circ}-\phi\) 且 \(\sin{x}=\sin{(90^{\circ}-\phi)}=\cos{\phi}=\frac{A}{\sqrt{A^2+B^2}}\)。
統計
\[ \begin{array}{lcccccccl} \text{sine} & \sin{\theta} & = & \frac{\text{opposite}}{\text{hypotenuse}} & \stackrel{\text{complementary}}{\leftrightarrow} & \cos{\theta} & = & \frac{\text{adjacent}}{\text{hypotenuse}} & \text{cosine} \\ \text{tangent} & \tan{\theta} & = & \frac{\text{opposite}}{\text{adjacent}} & \stackrel{\text{complementary}}{\leftrightarrow} & \cot{\theta} & = & \frac{\text{adjacent}}{\text{opposite}} & \text{cotangent}\\ \text{secant} & \sec{\theta} & = & \frac{\text{hypotenuse}}{\text{adjacent}} & \stackrel{\text{complementary}}{\leftrightarrow} & \csc{\theta} & = & \frac{\text{hypotenuse}}{\text{opposite}} & \text{cosecant} \end{array} \] \[ \begin{array}{lcccccccl} & \sin{\theta} & = & \frac{\text{opposite}}{\text{hypotenuse}} & \stackrel{\text{reciprocal}}{\leftrightarrow} & \csc{\theta} & = & \frac{\text{hypotenuse}}{\text{opposite}} \\ & \tan{\theta} & = & \frac{\text{opposite}}{\text{adjacent}} & \stackrel{\text{reciprocal}}{\leftrightarrow} & \cot{\theta} & = & \frac{\text{adjacent}}{\text{opposite}} \\ & \sec{\theta} & = & \frac{\text{hypotenuse}}{\text{adjacent}} & \stackrel{\text{reciprocal}}{\leftrightarrow} & \cos{\theta} & = & \frac{\text{adjacent}}{\text{hypotenuse}} \end{array} \]相關係數 \(r=\frac{S_{xy}}{\sqrt{S_{xx}}\sqrt{S_{yy}}}\) 絕對值小於1的證明（介於-1到1之間）
由柯西不等式 \[ (a_1 b_1+a_2 b_2+\cdots+a_n b_n)^2\leq (a_1^2+a_2^2+\cdots+a_n^2)(b_1^2+b_2^2+\cdots+b_n^2) \]
將 \(a_i, b_i\) 分別換成 \((x_i-\mu_x), (y_i-\mu_y)\)。
迴歸直線證明 Suppose the regression line is \(y={m}x+{c}\). We have to find \({m}\) and \({c}\) to minimize the following. \[ \begin{array}{lll} \sum_{i=1}^{n}[y_i-({m}x_i+{c})]^2 &=& \sum_{i=1}^{n}y_i^2-2y_i({m}x_i+{c})+({m}x_i+{c})^2 \\ &=& \sum_{i=1}^{n}y_i^2-2{m}x_i y_i-2{c}y_i+{m}^2 x_i^2+2{m}{c}x_i+{c}^2 \\ &=& \sum_{i=1}^{n}y_i^2-2{m}\sum_{i=1}^{n}x_i y_i-2{c}\sum_{i=1}^{n}y_i+{m}^2\sum_{i=1}^{n}x_i^2+2{m}{c}\sum_{i=1}^{n}x_i+\sum_{i=1}^{n}{c}^2 \\ &=& \sum_{i=1}^{n}y_i^2-2{m}\sum_{i=1}^{n}x_i y_i-2n{c}\mu_y+{m}^2\sum_{i=1}^{n}x_i^2+2n{m}{c}\mu_x+n{c}^2 \\ &\stackrel{\text{squre}}{=}& {m}^2\sum_{i=1}^{n}x_i^2-2{m}\sum_{i=1}^{n}x_i y_i+\sum_{i=1}^{n}y_i^2+n[{c}^2+2({m}\mu_x-\mu_y){c}] \\ &=& {m}^2\sum_{i=1}^{n}x_i^2-2{m}\sum_{i=1}^{n}x_i y_i+\sum_{i=1}^{n}y_i^2+n[{c}^2+2({m}\mu_x-\mu_y){c}+({m}\mu_x-\mu_y)^2]-n({m}\mu_x-\mu_y)^2 \\ &=& {m}^2\sum_{i=1}^{n}x_i^2-2{m}\sum_{i=1}^{n}x_i y_i+\sum_{i=1}^{n}y_i^2+n[{c}+({m}\mu_x-\mu_y)^2]-n{m}^2\mu_x^2+2n{m}\mu_x\mu_y-n\mu_y^2 \\ &\stackrel{\text{group x, y}}{=}& {m}^2(\sum_{i=1}^{n}x_i^2-n\mu_x^2)-2{m}(\sum_{i=1}^{n}x_i y_i-n\mu_x \mu_y)+(\sum_{i=1}^{n}y_i^2-n\mu_y^2)+n[{c}+({m}\mu_x-\mu_y)]^2 \\ &=& {m}^2 S_{xx}-2{m}S_{xy}+S_{yy}+n[{c}+({m}\mu_x-\mu_y)]^2 \\ &=& S_{xx}\left({m}^2-2{m}\frac{S_{xy}}{S_{xx}}\right)+S_{yy}+n[{c}+({m}\mu_x-\mu_y)]^2 \\ &=& S_{xx}\left({m}^2-2{m}\frac{S_{xy}}{S_{xx}}+\frac{S_{xy}^2}{S_{xx}^2}\right)+S_{yy}-\frac{S_{xy}^2}{S_{xx}}+n[{c}+({m}\mu_x-\mu_y)]^2 \\ &=& S_{xx}\left({m}-\frac{S_{xy}}{S_{xx}}\right)^2+S_{yy}-\frac{S_{xy}^2}{S_{xx}}+n[{c}+({m}\mu_x-\mu_y)]^2 \\ &=& S_{xx}\left({m}-\frac{S_{xy}}{S_{xx}}\right)^2+\frac{S_{xx}S_{yy}-S_{xy}^2}{S_{xx}}+n[{c}+({m}\mu_x-\mu_y)]^2. \end{array} \] minimum occurs at \({m}=\frac{S_{xy}}{S_{xx}}\) and \({c}=\mu_y-{m}\mu_x=\mu_y-\frac{S_{xy}}{S_{xx}}\mu_x\). Therefore, the regression line is \(y=mx+c=\frac{S_{xy}}{S_{xx}}x+\mu_y-\frac{S_{xy}}{S_{xx}}\mu_x\). That is, \[ y-\mu_y=\frac{S_{xy}}{S_{xx}}(x-\mu_x). \]
餘弦定理 \[ \begin{array}{rcl} \overline{CD}&=&b\cos{C},\\ \overline{AD}&=&b\sin{C},\\ \overline{DB}&=&a-b\cos{C}. \end{array} \] \[ \begin{array}{rcl} c^2 &=& \overline{AD}^2+\overline{DB}^2 \\ &=& (b\sin{C})^2+(a-b\cos{C})^2 \\ &=& b^2\sin^2{C}+a^2-2ab\cos{C}+b^2\cos^2{C} \\ &=& a^2+b^2-2ab\cos{C} \\ \cos{C}&=& \frac{a^2+b^2-c^2}{2ab} \end{array} \]
算幾不等式的證明
\(\frac{a+b}{2}\geq \sqrt{ab}\)
x的長度可以從圖中的三個直角三角形利用畢氏定理得到，也就是 \((x^2+a^2)+(x^2+b^2)=(a+b)^2\)。
設正實數a的純小數部分為b，已知a+b²=n，n為整數，求b
因為0<b<1，所以0<b²<1且n-1<a=n-b²<n，由此知a的整數部分為n-1。將a=(n-1)+b代入a+b²=n，得b²+b-1=0，解得b=(-1+√5)/2
相似題，相異解
第一題：∆ABC中，過A, B, C的三中線長依序為5, 6, 7，求∆ABC的面積為？8√6（對話式數2，p.236, exa.10.2）
解：令AM=5, BP=6, CN=7。以GB及GC為兩邊做平行四邊形GBDC，則GD=2GM=2*1/3*AM=10/3，BG=2/3*BP=4，BD=GC=2/3*CN=14/3，對∆BGD用海龍公式，得∆BGD面積為8√6/3。記得三角形三中線把三角形面積六等分，∆BGD面積佔了其中的兩份，所以∆ABC=3*∆BGD=8√6。
第二題：∆ABC的重心為G，已知GA=4, GB=5, GC=3，求邊長BC？2√13（對話式數2，p.238, exa.11.2）
解：由三角形中線的性質，AG:GM=2:1，所以GM=2，對∆BGC用中線定理，GB²+GC²=2(GM²+BM²)
由三中線求面積，由三高求面積（有沒有由三分角線求面積？）
第一題：∆ABC中，過A, B, C的三中線長依序為5, 6, 7，求∆ABC的面積為？8√6（對話式數2，p.236, exa.10.2）
第二題：設∆ABC過A的高為h_a=6，過B的高為h_b=3，過C的高為h_c=4，求∆ABC的面積為？16√15/5（對話式數2，p.237, exe.38）
由h_a:h_b:h_c得到a:b:c，再用一組底×高÷2=海龍公式。
設 \(\theta\) 為一銳角，且 \(\frac{1-\sin{\theta}}{1+\sin{\theta}}=2-\sqrt{3}\)，試求 \(\tan{\theta}+\cos{\theta}\) Ans: (3√2+2√3)/6 解法：設 \(x=\sin{\theta}\)，解 \(\frac{1-x}{1+x}=2-\sqrt{3}\)，得 \(x=\sin{\theta}=\frac{\sqrt{3}}{3}\)，接著畫銳角三角形。
∠C=90°, AC:BC=3:5, BD:CD=2:3, ∠BAD=θ, tan θ=?
由題設，BD=2r, CD=3r, AC=3r, AD=3√2r, AB=√34r
做AB邊上的高DE，由ABD=½*BD*AC=½*AB*DE，得到DE=(6/√34)r
接著如果再求AE才求tan θ=DE/AE，會很複雜。
所以我們要用別的方法，就是直接用sin θ求出tan θ，也就是sin θ=DE/AD及 \[ \tan^2{\theta}=\frac{\sin^2{\theta}}{\cos^2{\theta}}=\frac{\sin^2{\theta}}{1-\sin^2{\theta}} \]
一題好題目（龍騰小試身手3A中偏難第4回）：已知兩點A(2cosα, 2sinα), B(cosβ, sinβ)且α-β=60°，則線段AB的長度為Ans:√3
Area of Quadrilateral Formula，四邊形的面積公式（知道兩對角線長度及夾角）
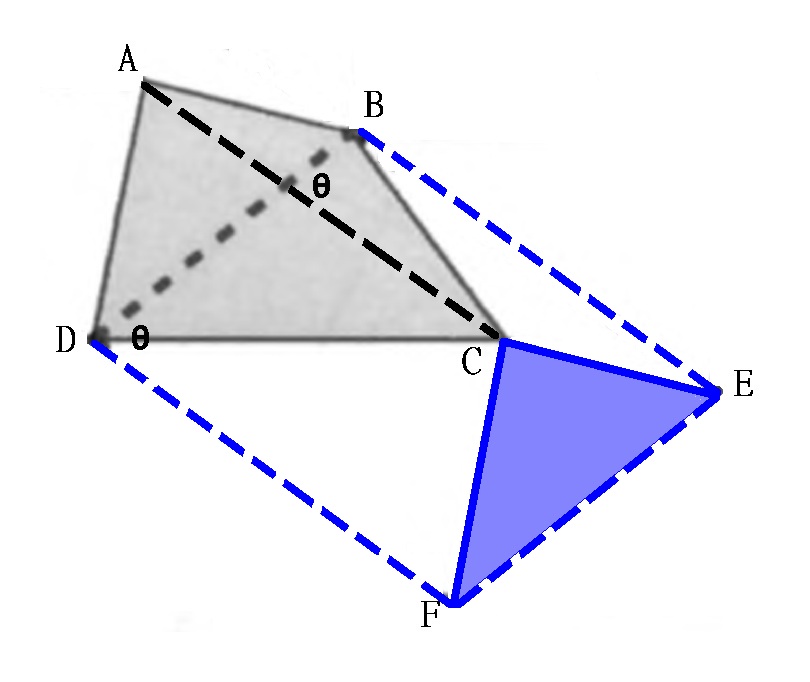
四邊形ABCD，做AC的平行線BE及DF，連接EF會與BD平行。於是 \[ ABCD=ABD+DBC=CEF+DBC=\frac{1}{2}\times BEFD=\frac{1}{2}\times 2\times BFD=\frac{1}{2}\times 2\times \frac{1}{2}\times BD\times DF\times \sin{\theta} \]
求過圓上一點的切線方程式用斜率
求過圓外一點的切線方程式用點線距
第一題：過圓(x-3)²+(y+2)²=29上的點(1,3)所作的切線方程式為Ans: -2x+5y=13（對話式數1, p.137, exa.3.1）
求圓心(3,-2)與點(1,3)的連線斜率，此半徑與切線垂直，由此得切線斜率，用點斜式得切線。
第二題：過圓C:(x-1)²+(y+2)²=25外一點P(8,-1)作圓C的兩條切線，求切線方程式為Ans: 3x+4y=20, 4x-3y=35（對話式數1, p.139, exa.5.1）
假設切線斜率為m，可假設切線方程為y-(-1)=m(x-8)，圓心到此切線的距離為半徑，用點線距公式求出m。
根軸公式的證明（ＯＯ高中陳Ｏ祥老師）
已知兩圓 \(C_1:f(x,y)=0\) 及 \(C_2:g(x,y)=0\) 相交於相異兩點 \(P(a,b)\) 及 \(Q(c,d)\)，則直線 \(\overleftrightarrow{PQ}\) 的方程式為 \(f(x,y)-g(x,y)=0\)。
證明：因為點 \(P\) 在圓 \(C_1\) 上，所以將點 \(P\) 的座標代入 \(f(x,y)\) 可以得到 \(f(a,b)=0\)。又因為點 \(P\) 也在圓 \(C_2\) 上，所以 \(g(a,b)=0\)。於是有 \(f(a,b)-g(a,b)=0-0=0\)，這表示點 \(P\) 在直線 \(f(x,y)-g(x,y)=0\) 上。
類似地，我們也可以得到點 \(Q\) 在直線 \(f(x,y)-g(x,y)=0\) 上。而兩點決定一條直線，所以 \(f(x,y)-g(x,y)=0\) 就是通過點 \(P\) 及點 \(Q\) 的直線方程式。
因數與倍數
用配對法求所有因數 用短除法求質因數分解 由質因數分解求所有因數 用短除法求最大公因數與最小公倍數， 用質因數分解求最大公因數與最小公倍數，
混合濃度問題（三杯雞）
濃度8%的食鹽水和濃度5%的食鹽水，各取多少克，可以混合成濃度6%的食鹽水300克。
用三個杯子來記，上面兩個杯子倒入下面的杯子
| ㄩ | ㄩ | |
| ㄩ |
比賽輸贏問題（井字法）
甲乙競賽，贏得2分，輸得1分，沒有平手，今甲得12分，乙得18分，試問比賽結果。
| 甲 | 乙 | |
| 贏 | x | y |
| 輸 | y | x |
巴斯卡定理（個人的記憶法）
\(\binom{n}{r}+\binom{n}{r+1}=\binom{n+1}{r+1}\)，上標為列，下標為行，注意到按照此編號排序，加的規則變成：上加下等於右下，一個L型。
| 10 | 11 | 12 | 13 | |
| 5 | \(\binom{10}{5}\) | |||
| 6 | \(\binom{10}{6}\) | |||
| 7 | \(\binom{11}{7}\) | |||
| 8 | \(\binom{12}{8}\) |
平行四邊形
| 平行四邊形 | ||
| 菱形（邊一樣） | ∩ | 長方形（角一樣） |
| 正方形 |
| parallelogram [͵pærəˋlɛlə͵græm] | ||
| rhombus [ˋrɑmbəs] | ∩ | rectangle |
| square |
| 四邊形\對角線 | 平分 | 垂直 | 等長 |
| 正方形 | V | V | V |
| 長方形 | V | V | |
| 平行四邊形 | V | ||
| 菱形 | V | V | |
| 箏形 | V |
\(9^{20}\)為幾位數？乘開後的最高位數為何？
\(\log{9^{20}}=20\log{9}=20\log{3^2}=40\log{3}=40\cdot 0.4771=19.084\)。
由log的定義，\(9^{20}=10^{19.084}=10^{19}\cdot 10^{0.084}\)，看一下0.084介在下表的哪兩個數中間。
\[ \begin{array}{rcl} \log{1} &=& 0 \\ \log{2} &=& 0.301 \\ \log{3} &=& 0.4771 \\ \log{5} &=& \log{\frac{10}{2}}=0.699 \\ \log{6} &=& \log{2}+\log{3}=0.778 \\ \log{7} &=& 0.8451 \\ \log{8} &=& \log{2^3}=0.903 \\ \log{9} &=& \log{3^2}=0.9542 \\ \end{array} \] 知道 \[ 0<0.084<0.301 \] 所以 \[ 1=10^0<10^{0.084}<10^{0.301}=2 \]所以 \(9^{20}\) 為一個20位數的數字，且 \(9^{20}\) 的最高位數為 \(1\)。
6件不同物品分給甲、乙、丙、丁四人，每人至少得1件，則有幾種分法。 全部-1人沒得+2人沒得-3人沒得 =4^6-C4,1*3^6+C4,2*2^6-C4,3*1^6 考慮3件不同物品分給A, B, C三人，每人至少得1件，則有幾種分法。 全部-1人沒得+2人沒得 =3^3-3*2^3+3*1^3 文華高一111下第二次 甲、乙、丙、丁、戊五人從左至右排成一列，甲不坐第一位且乙不坐第二位且丙不坐第三位且丁不坐第四位且戊不坐第五位的排法有5!-C5,1*4!+C5,2*3!-C5,3*2!+C5,4*1!-C5,5*0!=44種 這是推廣的排容原理\(C^5_1n(\text{甲第一})-C^5_2n(\text{甲第一}\cap \text{乙第二})+C^5_3n(\text{甲第一}\cap \text{乙第二}\cap \text{丙第三})+\cdots\)
下面這兩題是相同的解法。
從1到20的自然數中取出三個不同的數，則三數成等差的取法有多少種？
從1到20的自然數中取出兩個不同的數，則兩數和為偶數的取法有多少種？
聽說此解法取自徐氏數學，未驗證。
我的做法是按照公差 \(d=9, d=8, ..., d=1\) 來討論，並找出規律。
實力相當的甲、乙兩人比賽羽球單打，約定先勝3局者可得獎金4800元。現在已知第一局甲獲勝，則下列選項哪些是正確的？（多選）
(1) 甲再連勝兩局的機率為 \(\frac{1}{4}\) Ans: 正確
(2) 乙先勝3局的機率為 \(\frac{1}{8}\) Ans: 錯誤
(3) 甲獲勝的期望值為3600元 Ans: 錯誤
(4) 乙獲勝的期望值為1500元 Ans: 正確
(5) 若甲勝一局之後，比賽因故中止並且不再比賽，則甲應該分得3300元才算公平 Ans: 正確
實力相當，所以贏的機率各是1/2，畫樹枝圖。
轉移矩陣
| 後＼前 | 狀態A | 狀態B |
| 狀態A | P(A→A) | P(B→A) |
| 狀態B | P(A→B) | P(B→B) |
一列火車從第一車到第十車共有十節車廂，若要求此三節車廂兩兩不相銜接，則共有多少種方法？
先將不相鄰的三節車廂挑出，剩下七節車廂，有八個空隙，再把這三節車廂插空隙。
一開始看起來不能用插空隙，可是其實可以，例如下圖
| V | V | V | V | V | V | V | V | |||||||
| O | O | O | O | O | O | O |
| V | V | V | ||||||||||||
| O | O | O | O | O | O | O |
| 1 | 5 | 8 | ||||||||||||
| V | V | V | ||||||||||||
| O | O | O | O | O | O | O | ||||||||
| 2 | 3 | 4 | 6 | 7 | 9 | 10 |
有18本不同的書，按下述條件求其分法：
| 三堆不同數量（5, 6, 7） | 兩堆相同數量（5, 5, 8） | |
| 分三堆 | \(\binom{18}{5}\binom{13}{6}\binom{7}{7}\) | \(\binom{18}{5}\binom{13}{5}\binom{8}{8}\cdot \frac{1}{2!}\) |
| 不確定三人 | \(\binom{18}{5}\binom{13}{6}\binom{7}{7}\cdot 3!\) | \(\binom{18}{5}\binom{13}{5}\binom{8}{8}\cdot \frac{3!}{2!}\) |
| 確定三人 | \(\binom{18}{5}\binom{13}{6}\binom{7}{7}\) | \(\binom{18}{5}\binom{13}{5}\binom{8}{8}\) |
單淘汰賽
| ㄇ | ||||||
| ㄇ | ㄇ | |||||
| ㄇ | ㄇ | ㄇ | ㄇ |
| ㄇ | ||||||
| ㄇ | Γ | |||||
| ㄇ | ㄇ | | | ㄇ |
| ㄇ | ||||||
| Γ | Γ | |||||
| | | ㄇ | | | ㄇ |
有4相同紅球、2相同藍球及2相同綠球全分給5人，若每人可拿一顆球或兩顆不同顏色的球（但不可不拿），則共有幾種不同的分配方式。（台中一中105段考）
注意到，必有四人各拿一顆紅球，也就是必有一人沒拿紅球，沒拿紅球的這個人有五種選擇。 接著，沒拿紅球的這個人，他所拿到的球，有三種情形。 1. 只拿一顆藍球，把五個人拿的球用符號表示，例如 RRRRB BGG 表示第一個人拿RB，第二個人拿RG，第三個人拿RG，第四個人只拿R，第五個人只拿B 或是 RRRRB G BG 表示第一個人拿RG，第二個人只拿R，第三個人拿RB，第四個人拿RG，第五個人只拿B 所以有BGG三個字母在四個位置排列，有P4取3除以2=12，再乘以一開始的五，所以是60。 2. 只拿一顆綠球 跟情形一類似。 3. 拿一顆藍球一顆綠球，把五個人拿的球用符號表示，例如 RRRRB G B G 表示第一個人拿RG，第二個人只拿R，第三個人拿RB，第四個人只拿R，第五個人拿BG 所以變成BG兩個字母在四個位置排列，有P4取2種，再乘以一開始的五，所以是60。 總共180
甲袋內有3顆黑球，乙袋內有1顆紅球。從甲袋抽取兩顆球放進乙袋後，再從乙袋抽取兩顆球放進甲袋，稱為1次操作。 (1)1次操作後，紅球在乙袋的機率為。 (2)2次操作後，紅球在乙袋的機率為。甲袋的色球數只會有下列兩種情形：甲3黑、甲2黑1紅。 \[ \begin{array}{ll} & P(\text{甲從0紅變成0紅}) \\ =& P(\text{0R}\to\text{0R}) \\ =& P(\text{甲原本是3黑，2黑去乙，2黑回甲}) \\ =& \frac{1}{3} \end{array} \] \[ \begin{array}{ll} & P(\text{甲從0紅變成1紅}) \\ =& P(\text{0R}\to\text{1R}) \\ =& P(\text{甲原本是3黑，2黑去乙，1黑1紅回甲}) \\ =& \frac{2}{3} \end{array} \] \[ \begin{array}{ll} & P(\text{甲從1紅變成0紅}) \\ =& P(\text{1R}\to\text{0R}) \\ =& P(\text{甲原本是2黑1紅，1黑1紅去乙，2B回甲}) \\ =& \frac{2}{9} \end{array} \] \[ \begin{array}{ll} & P(\text{甲從1紅變成1紅}) \\ =& P(\text{1R}\to\text{1R}) \\ =& P(\text{甲原本是2黑1紅，2黑去乙，2黑回甲}) \\ +& P(\text{甲原本是2黑1紅，1黑1紅去乙，1黑1紅回甲}) \\ =& \frac{7}{9} \end{array} \] 令甲袋內紅球數機率行矩陣為 \(\begin{bmatrix}P(\text{0R})\\P(\text{1R})\end{bmatrix}\)，初狀態為 \(\begin{bmatrix}1\\0\end{bmatrix}\)，每次操作的轉移方陣為 \[ \begin{bmatrix} P(\text{0R}\to \text{0R})& P(\text{1R}\to \text{0R}) \\ P(\text{0R}\to \text{1R})& P(\text{1R}\to \text{1R}) \end{bmatrix} = \begin{bmatrix} \frac{1}{3}& \frac{2}{9} \\ \frac{2}{3}& \frac{7}{9} \end{bmatrix} \] 1次操作後紅球在甲袋的機率為 \(\frac{2}{3}\)，下面乘法向量的第二個分量。 \[ \begin{bmatrix} \frac{1}{3}& \frac{2}{9} \\ \frac{2}{3}& \frac{7}{9} \end{bmatrix} \begin{bmatrix} 1\\0 \end{bmatrix} = \begin{bmatrix} \frac{1}{3}\\\frac{2}{3} \end{bmatrix} \] 紅球在乙袋的機率為 \(1-\frac{2}{3}=\frac{1}{3}\)。
2次操作後紅球在甲袋的機率為 \(\frac{20}{27}\)，下面乘法向量的第二個分量。 \[ \begin{bmatrix} \frac{1}{3}& \frac{2}{9} \\ \frac{2}{3}& \frac{7}{9} \end{bmatrix} \begin{bmatrix} \frac{1}{3}\\\frac{2}{3} \end{bmatrix} = \begin{bmatrix} \frac{7}{27}\\\frac{20}{27} \end{bmatrix} \] 紅球在乙袋的機率為 \(1-\frac{20}{27}=\frac{7}{27}\)。 第一次操作時的情況。
| 第一種情況 | ||||||||
| 甲 | 乙 | 甲 | 乙 | 甲 | 乙 | |||
| ● | ● | 甲2黑到乙→ | ● | ● | 乙2黑回甲→ | ● | ● | |
| ● | ● | ● | ||||||
| ● | ● | ● | ||||||
| 第二種情況 | ||||||||
| 甲 | 乙 | 甲 | 乙 | 甲 | 乙 | |||
| ● | ● | 甲2黑到乙→ | ● | ● | 乙1黑1紅回甲→ | ● | ● | |
| ● | ● | ● | ||||||
| ● | ● | ● |
| 第一種情況 | ||||||||
| 甲 | 乙 | 甲 | 乙 | 甲 | 乙 | |||
| ● | ● | 甲2黑到乙→ | ● | ● | 乙2黑回甲→ | ● | ● | |
| ● | ● | ● | ||||||
| ● | ● | ● | ||||||
| 第二種情況 | ||||||||
| 甲 | 乙 | 甲 | 乙 | 甲 | 乙 | |||
| ● | ● | 甲2黑到乙→ | ● | ● | 乙1黑1紅回甲→ | ● | ● | |
| ● | ● | ● | ||||||
| ● | ● | ● | ||||||
| 第三種情況 | ||||||||
| 甲 | 乙 | 甲 | 乙 | 甲 | 乙 | |||
| ● | ● | 甲2黑到乙→ | ● | ● | 乙2黑回甲→ | ● | ● | |
| ● | ● | ● | ||||||
| ● | ● | ● | ||||||
| 第四種情況 | ||||||||
| 甲 | 乙 | 甲 | 乙 | 甲 | 乙 | |||
| ● | ● | 甲1黑1紅到乙→ | ● | ● | 乙2黑回甲→ | ● | ● | |
| ● | ● | ● | ||||||
| ● | ● | ● | ||||||
| 第五種情況 | ||||||||
| 甲 | 乙 | 甲 | 乙 | 甲 | 乙 | |||
| ● | ● | 甲1黑1紅到乙→ | ● | ● | 乙1黑1紅回甲→ | ● | ● | |
| ● | ● | ● | ||||||
| ● | ● | ● |
No comments:
Post a Comment